Trong các khẳng định sau, khẳng định nào đúng?
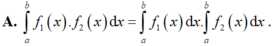
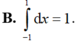
C. Nếu f(x) liên tục và không âm trên [a;b] thì ∫ a b f x d x ≥ 0
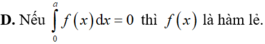
Cho hàm số f(x) liên tục trên ℝ và a là số dương. Trong các khẳng định sau, khẳng định nào đúng?
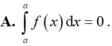
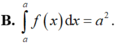
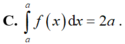
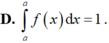
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên sau:
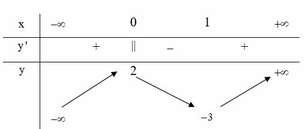
Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số có một cực tiểu và không có cực đại
B. Hàm số có giá trị cực tiểu bằng 1
C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3
D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1
Cho hàm số y=f(x) xác định, liên tục trên [-1;1] và có bảng biến thiên như sau.
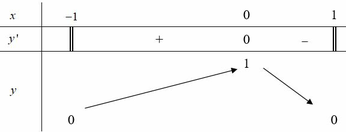
Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số có giá trị lớn nhất bằng 0
B. Hàm số có giá trị cực tiểu bằng 1
C. Hàm số đạt cực đại tại x=1
D. Hàm số có đúng một cực trị
Chọn D.
Dựa vào BBT ta thấy, hàm số có 1 điểm cực trị và đó là điểm cực đại.
Hàm số đạt cực đại tại x=0 và giá trị cực đại y c đ = 1 .
Hàm số đạt giá trị lớn nhất tại x=0 và GTLN là 1
Cho hàm số y = f(x) xác định, liên tục trên [-1; 1] và có bảng biến thiên như sau
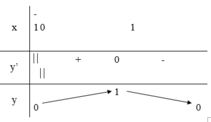
Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số có giá trị lớn nhất bằng 0
B. Hàm số có đúng một cực trị
C. Hàm số đạt cực đại tại x = 1
D. Hàm số có giá trị cực tiểu bằng 1.
Đáp án B
A sai do hàm số có giá trị lớn nhất bằng 1.
C, D sai do hàm số đạt cực đại tại x = 0 và giá trị cực đại y = 1
Cho hàm số y = f ( x ) liên tục trên R có bảng biến thiên
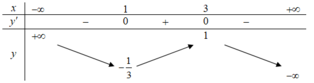
Trong các khẳng định sau, khẳng định nào là đúng?
A. Hàm số nghịch biến trên khoảng (1;3).
B. Hàm số đạt cực tiểu tại x = 3.
C. Hàm số có giá trị cực tiểu là - 1 3
D. Hàm số không có cực trị
Tìm khẳng định đúng trong các khẳng định sau:
( I ) f ( x ) = x 5 - x 2 + 1 liên tục trên R
( II ) f ( x ) = 1 x 2 - 1 liên tục trên khoảng (-1; 1).
( III ) f ( x ) = x - 2 liên tục trên đoạn [2; +∞).
A. Chỉ (I) đúng.
B. Chỉ (I) và (II).
C. Chỉ (II) và (III).
D. Chỉ (I) và (III).
Chọn D.
Ta có (I) đúng vì f(x) = x5 – x2 + 1 là hàm đa thức nên liên tục trên R..
Ta có (III) đúng vì ![]() liên tục trên (2; +∞) và
liên tục trên (2; +∞) và ![]() nên hàm số liên tục trên [2; +∞)
nên hàm số liên tục trên [2; +∞)
(!!) sai vì hàm số gián đoạn tại các điểm hàm số không xác định.
Tìm khẳng định đúng trong các khẳng định sau:
(I) f ( x ) = x + 1 x - 1 liên tục với mọi x ≠ 1
(II) f(x) = sinx liên tục trên R.
(III) f ( x ) = x x liên tục tại x = 1
A. Chỉ (I) đúng.
B. Chỉ (I) và (II).
C. Chỉ (I) và (III).
D. Chỉ (II) và (III).
Chọn B.
Ta có (II) đúng vì hàm số lượng giác liên tục trên từng khoảng của tập xác định.
Ta có (III) đúng vì 
Khi đó ![]()
Vậy hàm số 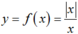 liên tục tại x = 1.
liên tục tại x = 1.
Xét hàm số f liên tục trên R và các số thực a, b, c tùy ý. Trong các khẳng định sau, khẳng định nào sai?
A. ∫ a b f x d x = ∫ c b f x d x - ∫ c a f x d x
B. ∫ a b f x d x = ∫ a c f x d x + ∫ c b f x d x
C. ∫ a b f x d x = ∫ a c f x d x - ∫ c b f x d x
D. ∫ a b f x d x = ∫ a c f x d x - ∫ b c f x d x
Cho hàm số . Tìm khẳng định đúng trong các khẳng định sau:
(I). f(x) liên tục tại x= 3
(II). f(x) gián đoạn tại x= 3 .
(III). f(x) liên tục trên R.
A. Chỉ (I) và (II).
B. Chỉ (II) và (III).
C. Chỉ (I) và (III).
D. Cả (I), (II), (III) đều đúng.
Chọn C.
Với ![]() ta có hàm số
ta có hàm số 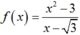 liên tục trên khoảng
liên tục trên khoảng ![]() và
và ![]() , (1).
, (1).
Với ![]() ta có
ta có ![]() và
và 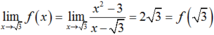 nên hàm số liên tục tại
nên hàm số liên tục tại ![]() , (2)
, (2)
Từ (1) và (2) ta có hàm số liên tục trên R.
Cho hàm số y=f(x) liên tục và có đạo hàm tới cấp hai trên a,b ; x 0 ∈ a ; b . Chọn khẳng định đúng trong các khẳng định sau:
A. Nếu f ' x 0 = 0 f ' ' x 0 < 0 thì x 0 là một điểm cực tiểu của hàm số
B. Nếu f ' x 0 = 0 f ' ' x 0 ≠ 0 thì x 0 là một điểm cực trị của hàm số.
C. Nếu f ' x 0 = 0 f ' ' x 0 > 0 thì x 0 là một điểm cực đại của hàm số
D. A, B, C đều sai.