Có bao nhiêu số thực b thuộc π ; 3 π sao cho ∫ a b 4 cos 2 x d x = 1
A. 0
B. 2
C. 4
D. 6
Có bao nhiêu số thực b thuộc π ; 3 π sao cho ∫ π b 4 c os 2 x d x = 1 ?
A. 8
B. 2
C. 4
D. 6
Đáp án C
Ta có ∫ π b 4 c os 2 x d x = 2 sin 2 x π b = 2 ⇔ sin 2 b = 1 sin 2 b = 1 2 ⇔ b = π 12 + k π b = 5 π 12 + k π k ∈ ℤ
b ∈ π ; 3 π ⇒ π < π 12 + k 1 π < 3 π π < 5 π 12 + k 2 π < 3 π ⇔ 11 12 < k 1 < 35 12 7 12 < k 2 < 31 12 ⇒ k 1 1 ; 2 k 2 1 ; 2
Suy ra có 4 giá trị thực của b thuộc π ; 3 π thỏa mãn đề bài.
Phương trình cos 2 x + cos x = 0 có bao nhiêu nghiệm thuộc khoảng − π ; π
A. 1
B. 4
C. 2
D. 3
Đáp án C.
Phương pháp
Sử dụng tính chất hai góc bù nhau cos x = cos π − x
Giải phương trình lượng giác cơ bản
Cách giải
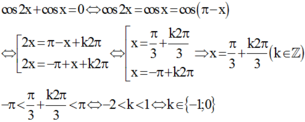
Vậy phương trình có 2 nghiệm thuộc − π ; π
Phương trình (sinx - cosx)(sinx + 2cosx - 3) = 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng - 3 π 4 ; π ?
A. 3
B. 0.
C. 1.
D. 2.
Có bao nhiêu số nguyên m sao cho phương trình msinx + 4cosx = 4 có nghiệm trong khoảng (0;π/3)?
A. 2.
B. 3.
C. 4.
D. 5.
Cho hàm số y = cos2x + sinx. Phương trình y’ = 0 có bao nhiêu nghiệm thuộc khoảng (0; π)
A. 1 nghiệm.
B. 2 nghiệm.
C. 3 nghiệm.
D. 4 nghiệm.
Chọn C.
y' = -2cosxsinx + cosx = cosx(1 – 2sinx)
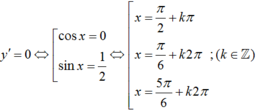
Vì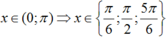 
. Vậy có 3 nghiệm thuộc khoảng (0; π).
Cho hàm số y = cos2x + sinx. Phương trình y’ = 0 có bao nhiêu nghiệm thuộc khoảng (0; π)
A. 1 nghiệm.
B. 2 nghiệm.
C. 3 nghiệm.
D. 4 nghiệm.
Cho a, b là các số thực thuộc khoảng ( 0 ; π / 2 ) và thỏa mãn điều kiện cota-tan( π / 2 -b)=a-b. Tính giá trị của biểu thức P = 3 a + 7 b a + b
A. P=5
B. P=2
C. P=4
D. P=6
