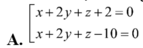
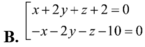
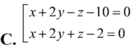
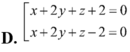
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 3x-2y-z+5=0 và đường thẳng ∆ : x - 1 2 = y - 7 1 = z - 3 4 . Gọi (Q) là mặt phẳng chứa đường thẳng ∆ và song song với (P). Tính khoảng cách giữa hai mặt phẳng (P) và (Q).
A. 9 14
B. 9 14
C. 3 14
D. 3 14
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng song song ( P ) : x − 2 y − 2 z + 1 = 0 và mặt phẳng ( Q ) : x − 2 y − 2 z − 2 = 0 . Khoảng cách h giữa hai mặt phẳng (P) và (Q) bằng bao nhiêu?
A. h = 1
B. h = 3
C. h = 1 3
D. h = 2 3
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng ( Q ) : x + 2 y - 2 z + 1 = 0 và cách (Q) một khoảng bằng 3.
A. x + 2 y - 2 z + 8 = 0 v à x + 2 y – 2 z – 10 = 0 .
B. x + 2 y - 2 z + 6 = 0 v à x + 2 y - 2 z – 8 = 0
C. x + 2 y – 2 z – 8 = 0 v à x + 2 y – 2 z + 10 = 0
D. Đáp án khác.
Chọn C.
Trên mặt phẳng (Q): x + 2y - 2z + 1 = 0 chọn điểm M (-1;0;0).
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng: x + 2y - 2z + D = 0 với D ≠ 1.
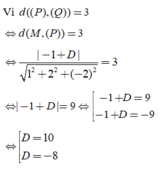
Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z + 10 = 0 và x + 2y -2z – 8 = 0.
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng ( Q ) : x + 2 y - 2 z + 1 = 0 và cách (Q) một khoảng bằng 3.
A. x + 2 y - 2 z + 8 = 0 v à x + 2 y – 2 z – 10 = 0 .
B. x + 2 y - 2 z + 6 = 0 v à x + 2 y - 2 z – 8 = 0
C. x + 2 y – 2 z – 8 = 0 v à x + 2 y – 2 z + 10 = 0
D. Đáp án khác.
Chọn C.
Trên mặt phẳng (Q): x + 2y - 2z + 1 = 0 chọn điểm M (-1;0;0).
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng: x + 2y - 2z + D = 0 với D ≠ 1.
Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z + 10 = 0 và x + 2y -2z – 8 = 0.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng Q : x + 2 y + 2 z - 3 = 0 , mặt phẳng (P) không qua O, song song với mặt phẳng (Q) và d : P ; Q = 1 . Phương trình mặt phẳng (P) là
A. x + 2 y + 2 z + 1 = 0
B. x + 2 y + 2 z = 0
C. x + 2 y + 2 z - 6 = 0
D. x + 2 y + 2 z + 3 = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q): x+2y+2z-3=0, mặt phẳng (P) không qua O, song song với mặt phẳng (Q) và d((P);(Q))=1. Phương trình mặt phẳng (P) là
Trong không gian Oxyz, cho mặt phẳng ( P ) : x + 2 y + 2 z - 10 = 0 . Phương trình mặt phẳng (Q) song song với (P) và khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 7 3 là
A. x + 2 y + 2 z - 3 = 0 ; x + 2 y + 2 z - 17 = 0
B. x + 2 y + 2 z + 3 = 0 ; x + 2 y + 2 z + 17 = 0
C. x + 2 y + 2 z + 3 = 0 ; x + 2 y + 2 z - 17 = 0
D. x + 2 y + 2 z - 3 = 0 ; x + 2 y + 2 z + 17 = 0
Trong không gian Oxyz, cho mặt phẳng (P): x+2y+2z-10 = 0. Phương trình mặt phẳng (Q) song song với (P) và khoảng cách giữa hai mặt phẳng (Q) và (P) bằng 7 3 là
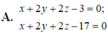
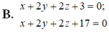
Trong không gian với hệ tọa độ Oxyz, cho điểm A(-2;1;5), mặt phẳng (P) : \(2x-2y+z-1=0\) và đường thẳng (d)\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z}{1}\). Tính khoảng cách từ A đến (P). Viết phương trình mặt phẳng (Q) đi qua A, vuông góc với (P) và song song với d.
Kẻ \(SH\perp AC\left(H\in AC\right)\)
Do \(\left(SAC\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(SA=\sqrt{AC^2-SC^2}=a;SH=\frac{SA.SC}{AC}=\frac{a\sqrt{3}}{2}\)
\(S_{ABCD}=\frac{AC.BD}{2}=2a^2\)
\(V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.2a^2=\frac{a^3\sqrt{3}}{3}\)
Ta có \(AH=\sqrt{SA^2-SH^2}=\frac{a}{2}\Rightarrow CA=4HA\Rightarrow d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Do BC//\(\left(SAD\right)\Rightarrow d\left(B,\left(SAD\right)\right)=d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Kẻ \(HK\perp AD\left(K\in AD\right),HJ\perp SK\left(J\in SK\right)\)
Chứng minh được \(\left(SHK\right)\perp\left(SAD\right)\) mà \(HJ\perp SK\Rightarrow HJ\perp\left(SAD\right)\Rightarrow d\left(H,\left(SAD\right)\right)=HJ\)
Tam giác AHK vuông cân tại K\(\Rightarrow HK=AH\sin45^0=\frac{a\sqrt{2}}{4}\)
\(\Rightarrow HJ=\frac{SH.HK}{\sqrt{SH^2+HK^2}}=\frac{a\sqrt{3}}{2\sqrt{7}}\)
Vậy \(d\left(B,\left(SAD\right)\right)=\frac{2a\sqrt{3}}{\sqrt{7}}=\frac{2a\sqrt{21}}{7}\)
