Gọi S là tập các giá trị m thỏa mãn hàm số y = m x 4 + m − 1 x 2 + 1 + 3 m chỉ có đúng một cực trị. Khi đó tập S là
A. S = [0;1)
B. S = 1 ; + ∞
C. S = − ∞ ; 0
D. S = − ∞ ; 0 ∪ 1 ; + ∞
Những câu hỏi liên quan
Xét hàm số
f
(
t
)
9
t
9
t
+
m
2
với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) 1 với mọi số thực x, y thỏa mãn
e
x
+
y...
Đọc tiếp
Xét hàm số f ( t ) = 9 t 9 t + m 2 với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) =1 với mọi số thực x, y thỏa mãn e x + y ≤ e ( x + y ) . Tìm số phần tử của S.
A. 0
B. 1
C. Vô số
D. 2
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số
Gọi S là tập các gí trị m là số nguyên để hàm số
y
1
3
x
2
-
m
+
1
x
2
+
m
-
2
x
+
2
m
-
3
đạt cực trị tại hai điểm
x
1
,...
Đọc tiếp
Gọi S là tập các gí trị m là số nguyên để hàm số y = 1 3 x 2 - m + 1 x 2 + m - 2 x + 2 m - 3 đạt cực trị tại hai điểm x 1 , x 2 thỏa mãn x 1 2 + x 2 2 = 18 . Tính tổng P của các giá trị nguyên m của S
A. P = - 4
B. P = 1
C. P = - 3 2
A. P = - 5
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 ; e 2 y = 1 . Số phần tử của S là:/
A. 0
B. 1
C. 2
D. Vô số
Chọn B
Cách giải: Ta có:
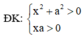
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
Đúng 0
Bình luận (0)
Gọi S là tập các giá trị dương của tham số m sao cho hàm số
y
x
3
-
3
m
x
2
+
9
x
-
m
đạt cực trị tại
x
1
,
x
2
thỏa mãn
x...
Đọc tiếp
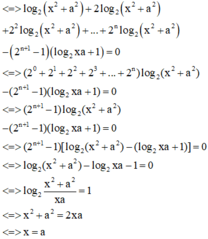
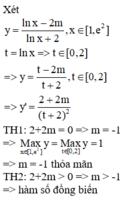
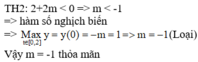
Gọi S là tập các giá trị dương của tham số m sao cho hàm số y = x 3 - 3 m x 2 + 9 x - m đạt cực trị tại x 1 , x 2 thỏa mãn x z - x 2 ≤ 2 Biết S=(a; b] Tính T= b-a
A. T = 1 + 3
B. T= 2 - 3
C. T= 2 + 3
D. T= 3 - 3
Gọi S là tập các giá trị dương của tham số m sao cho hàm số
y
x
3
-
3
m
x
2
+
9
x
-
m
đạt cực trị tại
x
1
,
x
2
thỏa mãn
x
1
-
x...
Đọc tiếp
Gọi S là tập các giá trị dương của tham số m sao cho hàm số y = x 3 - 3 m x 2 + 9 x - m đạt cực trị tại x 1 , x 2 thỏa mãn x 1 - x 2 ≤ 2 . Biết S=(a;b]. Tính T=b-a
Gọi S là tập các giá trị dương của tham số m sao cho hàm số
y
x
3
−
3
m
.
x
2
+
9
x
−
m
đạt cực trị tại
x
1
,
x
2
thỏa mãn
x
1
−
x...
Đọc tiếp
Gọi S là tập các giá trị dương của tham số m sao cho hàm số y = x 3 − 3 m . x 2 + 9 x − m đạt cực trị tại x 1 , x 2 thỏa mãn x 1 − x 2 ≤ 2. Biết S = a ; b . Tính T = b − a
A. T = 2 + 3
B. T = 1 + 3
C. T = 2 − 3
D. T = 3 − 3
cho hàm số y=x2 - mx - m - 1 (m ϵ R) . Gọi S là tập hợp tất cả các giá trị của m để đồ thị đã cho cắt trục hoành tại 2 điểm phân biệt có hoành độ x1 ; x2 thỏa mãn |x1|+|x2|=4 . Tổng tất cả các phần tử của S là bao nhiêu
Cho các số thực x, y thay đổi thỏa mãn
x
2
+
y
2
-
x
y
1
và hàm số
f
t
2
t
3
-
3
t
2
-
1
. Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của
Q
f...
Đọc tiếp
Cho các số thực x, y thay đổi thỏa mãn x 2 + y 2 - x y = 1 và hàm số f t = 2 t 3 - 3 t 2 - 1 . Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của Q = f 5 x - y + 2 x + y + 4 . Tổng M + m bằng
A. - 4 - 3 2
B. - 4 - 5 2
C. - 4 - 4 2
D. - 4 - 2 2
