Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường y = 1 x − 3 , y = 0 , x = 0 , x = 2 quay một vòng quanh trục Ox là (theo đơn vị thể tích)
A. 2 π
B. 2 3 π
C. 4 3 π
D. 1 3 π
Những câu hỏi liên quan
Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường
y
1
x
-
3
, y 0; x 0; x 2 quay một vòng quanh trục Ox là A.
2
π
B.
2
π
3
C.
4
π
3...
Đọc tiếp
Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường y = 1 x - 3 , y = 0; x = 0; x= 2 quay một vòng quanh trục Ox là
A. 2 π
B. 2 π 3
C. 4 π 3
D. π 3
Tính thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường y=x^2-3x+2;y=x+2 quay quanh ox
Pt hoành độ giao điểm: \(x^2-3x+2=x+2\Leftrightarrow x^2-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
\(x^2-3x+2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
\(\Rightarrow V=\pi\left(\int\limits^4_0\left(x+2\right)^2dx-\int\limits^1_0\left(x^2-3x+2\right)^2dx-\int\limits^4_2\left(x^2-3x+2\right)^2dx\right)\)
\(=\pi\left(\dfrac{208}{3}-\dfrac{5}{6}-\dfrac{14}{3}\right)=\dfrac{383\pi}{6}\)
Đúng 1
Bình luận (2)
Thể tích khối tròn xoay sinh bởi hình phẳng (H) quay quanh trục Ox biết hình (H) giới hạn bởi các đường y lnx; y x; x1;
x
e
2
là:
Đọc tiếp
Thể tích khối tròn xoay sinh bởi hình phẳng (H) quay quanh trục Ox biết hình (H) giới hạn bởi các đường y = lnx; y =x; x=1; x = e 2 là:
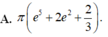
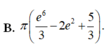
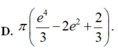
Thể tích khối tròn xoay sinh bởi hình phẳng (H) quay quanh trục Ox là:
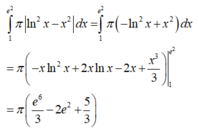
Đáp án B
Đúng 0
Bình luận (0)
Thể tích khối tròn xoay sinh bởi hình phẳng (H) quay quanh trục Ox biết hình (H) giới hạn bởi các đường ylnx, yx, x1,
x
e
2
là A.
π
.
(
e
5
+
2
e
2
+
2
3
)
B.
π
.
(
e
6
3...
Đọc tiếp
Thể tích khối tròn xoay sinh bởi hình phẳng (H) quay quanh trục Ox biết hình (H) giới hạn bởi các đường y=lnx, y=x, x=1, x = e 2 là
A. π . ( e 5 + 2 e 2 + 2 3 )
B. π . ( e 6 3 - 2 e 2 + 5 3 )
C. π . ( e 5 - 2 e 2 + 2 )
D. π . ( e 4 3 - 2 e 2 + 2 3 )
Tính thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường by=x^2/4, y=2x quay quanh Ox
Pt hoành độ giao điểm:
\(\dfrac{x^2}{4}=2x\Rightarrow\left[{}\begin{matrix}x=0\\x=8\end{matrix}\right.\)
\(\Rightarrow V=\pi\left(\int\limits^8_0\left(2x\right)^2dx-\int\limits^8_0\left(\dfrac{x^2}{4}\right)^2dx\right)=\dfrac{4096\pi}{15}\)
Đúng 2
Bình luận (1)
Thể tích khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi các đường
y
x
3
,
t
r
ụ
c
O
x
,
x
-
1
,
x
1
một vòng quanh trục Ox là: A.
π
B.
2
π
C.
6
π
7...
Đọc tiếp
Thể tích khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi các đường y = x 3 , t r ụ c O x , x = - 1 , x = 1 một vòng quanh trục Ox là:
A. π
B. 2 π
C. 6 π 7
D. 2 π 7
Chọn D.
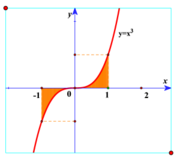
Thể tích khối tròn xoay được giới hạn bởi các đường y = x3, trục Ox, x = -1, x = 1 một vòng quanh trục Ox là:
Đúng 0
Bình luận (0)
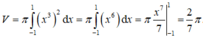
Tính thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi các đường y=e^x/4, trục ox, x=0,x=4 quay quanh ox
\(V=\pi\int\limits^4_0\left(\dfrac{e^x}{4}\right)^2dx=\pi\int\limits^4_0\dfrac{e^{2x}}{16}dx=\dfrac{\pi}{32}.e^{2x}|^4_0=\dfrac{\pi}{32}\left(e^8-1\right)\)
Đúng 0
Bình luận (0)
Cho hình phẳng (H) giới hạn bởi đồ thị các hàm số sau
y
x
,
y
1
đường thẳng x 4 (tham khảo hình vẽ). Thể tích khối tròn xoay sinh bởi hình (H) khi quay quanh đường thẳng y 1 bằng A.
9
2
π
B.
119
6
π
C.
7
6
π
D.
21
2...
Đọc tiếp
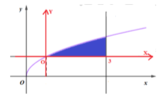
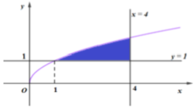
Cho hình phẳng (H) giới hạn bởi đồ thị các hàm số sau y = x , y = 1 đường thẳng x = 4 (tham khảo hình vẽ). Thể tích khối tròn xoay sinh bởi hình (H) khi quay quanh đường thẳng y = 1 bằng
A. 9 2 π
B. 119 6 π
C. 7 6 π
D. 21 2 π
Chọn C.
Ta được hệ trục tọa độ OXY như hình vẽ:
Đúng 0
Bình luận (0)
Cho hình phẳng (H) giới hạn bởi đồ thị các hàm số sau
y
x
, y1 đường thẳng x4 (tham khảo hình vẽ). Thể tích khối tròn xoay sinh bởi hình (H) khi quay quanh đường thẳng y1 bằng
Đọc tiếp
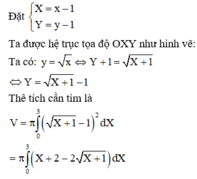
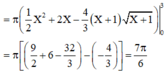
Cho hình phẳng (H) giới hạn bởi đồ thị các hàm số sau y = x , y=1 đường thẳng x=4 (tham khảo hình vẽ). Thể tích khối tròn xoay sinh bởi hình (H) khi quay quanh đường thẳng y=1 bằng
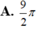
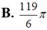
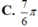
