Tính môđun của số phức z biết z → = 4 − 3 i 1 + i .
A. z = 25 2 .
B. z = 7 2 .
C. z = 5 2 .
D. z = 2 .
Những câu hỏi liên quan
Tính môđun của số phức z biết z ¯ = (4-3i)(1+i).
A. |z| = 25 2
B. |z| = 7 2
C. |z| = 5 2
D. |z| = 2
Đáp án C
Cách 1: Áp dụng quy tắc nhân, em tính được
Cách 2:
Áp dụng công thức giải nhanh: 
= 5 2
Em ấn MODE 2 SHIFT hyp (để tính mô đun) nhập (4-3i)(1+i) =
Em được kết quả là 5 2
Đúng 0
Bình luận (0)
Cho số phức
z
i
+
1
n
, biết
n
∈
ℤ
và thỏa mãn
log
2
8
-
n
+
log
2
n
+
3
log
2...
Đọc tiếp
Cho số phức z = i + 1 n , biết n ∈ ℤ và thỏa mãn log 2 8 - n + log 2 n + 3 = log 2 10 .
Tính môđun của số phức z.
A. 2
B. 4 2
C. 8
D. z = 8 2 h o ặ c z = 1 2
Cho số phức z thỏa mãn
z
+
(
2
+
i
)
z
¯
3
+
5
i
. Tính môđun của số phức z.
Đọc tiếp
Cho số phức z thỏa mãn z + ( 2 + i ) z ¯ = 3 + 5 i . Tính môđun của số phức z.
Tìm môđun của số phức z biết z-4 = (1+i)|z| - (4+3z)i.
A. |z| = 4
B. |z| = 1
C. |z| = 1 2
D. |z| = 2
Tìm môđun của số phức z biết z - 4 = (1 + i)|z| - (4+3z)i
A. |z| = 4
B. |z| = 1
C. |z| = 1 2
D. |z| = 2
Cho số phức z thỏa mãn điều kiện
z
-
3
+
2
i
z
-
i
Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
Biết số phức z thỏa mãn đồng thời hai điều kiện
z
-
3
-
4
i
5
và biểu thức
M
|
z
+
2
|
2
-
|
z
-
i
|
2
đạt giá tri lớn nhất. Tính môđun của số phức z+i
Đọc tiếp
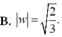
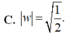
Biết số phức z thỏa mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = | z + 2 | 2 - | z - i | 2 đạt giá tri lớn nhất. Tính môđun của số phức z+i
Câu 1 : Cho số phức z thỏa mãn z + ( 2 - i )overline{z} 3 - 5i. Môđun của số phức w z - i bằng bao nhiêu ?Câu 2 : Cho số phức z a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )z + ( 2 - i )2 4 + i. Tính P a - b
Đọc tiếp
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Biết số phức z thỏa mãn đồng thời hai điều kiện:
z
-
3
-
4
i
5
và biểu thức
M
z
+
2
2
-
z
-
i
2...
Đọc tiếp
Biết số phức z thỏa mãn đồng thời hai điều kiện: z - 3 - 4 i = 5 và biểu thức M = z + 2 2 - z - i 2 đạt giá trị lớn nhất. Tính môđun của số phức z +i.
A. z + i = 61
B. z + i = 5 2
C. z + i = 3 5
D. z + i = 2 41
