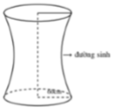
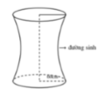
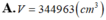
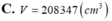
Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục lơn bằng 80cm, độ dài trục bé bằng 60cm. Tính thể tích V của trống (kết quả làm tròn đến hàng đơn vị)
A. V = 344963 c m 3
B. V = 344964 c m 3
C. V = 208347 c m 3
D. V = 208346 c m 3
Chọn B.
Phương pháp:
Sử dụng công thức ứng dụng tích phân để tích thể tích khối tròn xoay.
Cách giải:
(Do phần đồ thị được lấy nằm phía dưới đường thẳng y = 60)
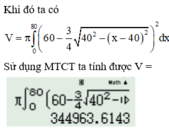
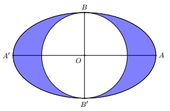
Trong mặt phẳng, cho đường elip (E) có độ dài trục lớn là AA’=10, độ dài trục nhỏ là BB’=6, đường tròn tâm O có đường kính là BB’ (như hình vẽ bên dưới). Tính thể tích V của khối tròn xoay có được bằng cách cho miền hình hình phẳng giới hạn bởi đường elip và được tròn (được tô đậm trên hình vẽ) quay xung quanh trục AA’
A. 
.
B. 
.
C. 
.
D. 
.
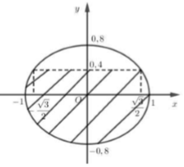
Người ta sử dụng xe bồn để chở dầu. Thùng đựng dầu có thiết diện ngang (mặt trong của thùng) là một đường elip có độ dài trục lớn bằng 2m , độ dài trục bé bằng 1, 6m , chiều dài (mặt trong của thùng) bằng 3, 5m . Thùng được đặt sao cho trục bé nằm theo phương thẳng đứng (như hình bên). Biết chiều cao của dầu hiện có trong thùng (tính từ điểm thấp nhất của đáy thùng đến mặt dầu) là 1, 2m . Tính thể tích V của dầu có trong thùng (Kết quả làm tròn đến hàng phần trăm).
A. V = 4 , 42 m 3
B. V = 2 , 02 m 3
C. V = 7 , 08 m 3
D. V = 2 , 31 m 3
Đáp án C
Phương pháp
- Gắn hệ trục tọa độ lên mặt thiết diện ngang. Viết phương trình elip.
- Tính diện tích phần thiết diện chỉ chứa dầu.
- Tính thể tích phần dầu trong thùng, sử dụng công thức V = Sh với S là diện tích một phần elip tính được ở trên, h là chiều dài của thùng chứa dầu.
Cách giải:
Chọn hệ trục tọa độ như hình vẽ
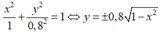
Diện tích thiết diện có chứa dầu là phần diện tích được
gạch chéo trong hình.
Ta tính diện tích phần không gạch chéo S1 là phần hình
phẳng giới hạn bởi đường thẳng y = 0, 4 với một phần elip
phía trên trục hoành có phương trình
Trong mặt phẳng (P), cho elip (E) có độ dài trục lớn AA’=8 và độ dài trục nhỏ là BB’=6. Đường tròn tâm O đường kính BB’ như hình vẽ. Tính thể tích vật thể tròn xoay có được bằng cách cho miền hình phẳng giới hạn bởi đường elip và đường tròn đó (phần hình phẳng tô đậm trên hình vẽ) quay xung quanh trục AA’
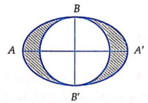
A. V = 36 π
B. V = 12 π
C. V = 16 π
D. V = 64 π 3 .
Trong mặt phẳng (P), cho elip (E) có độ dài trục lớn AA'=8 và độ dài trục nhỏ là BB'=6. Đường tròn tâm O đường kính BB’ như hình vẽ. Tính thể tích vật thể tròn xoay có được bằng cách cho miền hình phẳng giới hạn bởi đường elip và đường tròn đó (phần hình phẳng tô đậm trên hình vẽ) quay xung quanh trục AA’
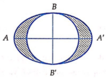
A. V = 36 π
B. V = 12 π
C. V = 16 π
D. V = 64 π 3 .
Đáp án B
Thể tích của khối tròn xoay thu được khi quay elip có trục lớn A A ' = 8 , trục nhỏ B B ' = 6 khi quay quanh trục AA’ là V E = 4 3 π . A A ' 2 . B B ' 2 2 = 4 3 π .4.3 2 = 48 π (đvtt).
Thể tích khối tròn xoay thu được khi quay đường tròn O ; B B ' 2 quanh trục AA’ cũng chính là thể tích khối cầu tâm O, bán kính R = 3 . Thể tích đó là
V O ; 3 = 4 3 π R 3 = 4 3 π .3 3 = 36 π (đvtt).
Vậy thể tích khối tròn xoay cần tính là V = V E − V O ; 3 = 48 π − 36 π = 12 π (đvtt)
Hình bên gồm đường tròn bán kính 3 và elip có độ dài trục lớn là 6, độ dài trục bé bằng 4 cắt nhau. Biết chiều dài nhất của hình bằng 11, tính diện tích của hình này
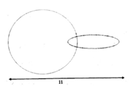
A. 46,24
B. 45,36
C. 47,28
D. 49,21
Một khuôn viên dạng nửa hình tròn, trên đó người ta thiết kế 2m, độ dài trục bé bằng 1m, chiều dài (mặt trong của thùng) bằng 3,5m.Thùng được đặt sao cho trục bé nằm theo phương thẳng đứng (như hình bên). Biết chiều cao của dầu hiện có trong thùng (tính từ điểm thấp nhất của đáy thùng đến mặt dầu) là 0,75m. Tính thể tích của dầu có trong thùng (Kết quả làm tròn đến hàng phần trăm).
A. V = 4 , 42 m 3
B. V = 3 , 23 m 3
C. V = 1 , 26 m 3
D. V = 7 , 08 m 3
Người ta cần cắt một tấm tôn có hình dạng là một elip với độ dài trục lớn bằng 2a, độ dài trục bé bằng 2 b a > b > 0 để được một tấm tôn hình chữ nhật nội tiếp elip. Người ta gò tấm tôn hình chữ nhật thu được một hình trụ không có đáy (như hình bên). Tính thể tích lớn nhất có thể thu được của khối trụ đó.
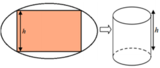
A. 2 a 2 b 3 2 π
B. 2 a 2 b 3 3 π
C. 4 a 2 b 3 2 π
D. 4 a 2 b 3 3 π
Đáp án B
Gọi R, h lần lượt là bán kính đáy và chiều cao của khối trụ
Chọ hệ trục tọa độ Oxy như hình vẽ với tứ giác ABCD là hình chữ nhật nối tiếp hình (E)
Gọi A x 0 ; y 0 x 0 > y 0 > 0 , khi đó ta có A B = 2 π R C D = h ⇔ 2 x 0 = 2 π R 2 y 0 = h ⇔ x 0 = π R y 0 = h 2
Thể tích khối trụ là V = π R 2 h = 2 x 0 2 π . y 0 mà A ∈ E ⇒ x 0 2 a 2 + y 0 2 b 2 = 1 ⇒ x 0 2 = a 2 b 2 b 2 − y 0 2
Bác Minh có một mảnh vườn hình Elip có độ dài trục lớn là 10m và độ dài trục nhỏ là 8m Giữa vườn là một cái giếng hình tròn có bán kính 0,5m và nhận trục lớn và trục bé của đường Elip làm trục đối xứng (như hình vẽ).
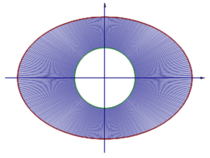
Bác Minh muốn trồng hoa hồng đỏ trên phần dải đất còn lại (xung quanh giếng). Biết kinh phí trồng hoa là 120.000 đồng/ m 2 . Hỏi Bác Minh cần bao nhiêu tiền để trồng hoa trên giải đất đó? (Số tiền làm tròn đến hàng nghìn)
A. 7.545.000 đồng
B. 7.125000 đồng
C. 7.325000 đồng
D. 7.446.000 đồng
