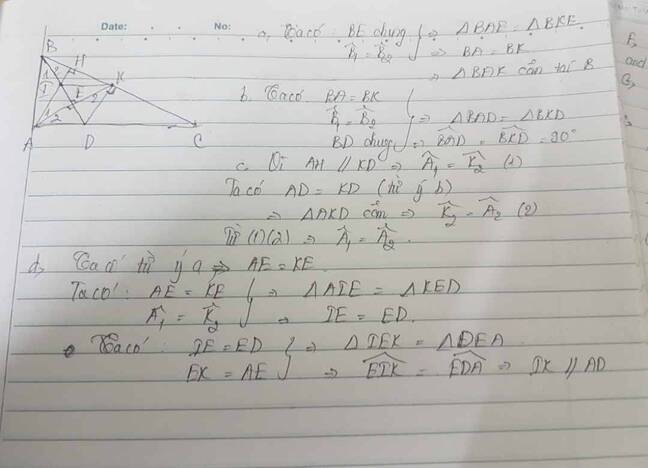Cho tam giác ABC cân tại A có A = 1000. Vẽ phân giác BD. Chứng minh rằng BD + BA = BC.

Những câu hỏi liên quan
1 ) Cho tam giác cân ABC . Vẽ AH ⊥ BC tại H . Chứng minh rằng :
a ) AH là tia phân giác của góc A
b ) HB = HC
2 ) Cho tam giác ABC cân tại A . Vẽ BD ⊥ AC , CE ⊥ AB . Chứng minh rằng : BD = CE
Bạn tự vẽ hình nha
1. a) ta có: tg abc cân => AB=AC; AH vừa là trung tuyến vừa là phân giác của tg abc (1)
=> AH là tia phân giác của góc A
b) từ (1) => AH là trung tuyến của tg abc
=> HB=HC
2. ta có: tg abc cân; ab=ac
=> bd và ce vừa là đường cao vừa là trung tuyến của tg abc
=> ad=dc; ab=be ( mà ab=ac)
=> ae=ad
tg abd= tg ace: ab=ac; góc a chung; ae=ad
=> bd=ce
học tốt nha bạn
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC), BD là đường phân giác. Vẽ DE vuông góc với BC tại E.
a) Cho biết AB = 6cm, AC = 8cm. Tính BC.
b) Chứng minh tam giác DAE cân.
c) Chứng minh rằng DA < DC.
d) Vẽ CF vuông góc với BD tại F. Chứng minh rằng các đường thẳng AB, DE, CF đồng quy.
Cho tam giác ABC vuông tại A, vẽ tia phân giác BD . Kẻ DE vuông góc với BC (
E thuộc BC ). Gọi F là giao điểm của BA và ED . Chứng minh rằng:
a) Tam giác bed bằng tam giác BAD .
b) Tam BCF cân tại b.
c) BD là đường trung tuyến của tam giác BCF .
Đọc tiếp
Cho tam giác ABC vuông tại A, vẽ tia phân giác BD . Kẻ DE vuông góc với BC (
E thuộc BC ). Gọi F là giao điểm của BA và ED . Chứng minh rằng:
a) Tam giác bed bằng tam giác BAD .
b) Tam BCF cân tại b.
c) BD là đường trung tuyến của tam giác BCF .
Cho tam giác ABC vuông tại A, vẽ tia phân giác BD . Kẻ DE vuông góc với BC (
E thuộc BC ). Gọi F là giao điểm của BA và ED . Chứng minh rằng:
a) Tam giác BED bằng tam giác BAD .
b) Tam BCF cân tại B .
c) BD là đường trung tuyến của tam giác BCF .
Đọc tiếp
Cho tam giác ABC vuông tại A, vẽ tia phân giác BD . Kẻ DE vuông góc với BC (
E thuộc BC ). Gọi F là giao điểm của BA và ED . Chứng minh rằng:
a) Tam giác BED bằng tam giác BAD .
b) Tam BCF cân tại B .
c) BD là đường trung tuyến của tam giác BCF .
Cho tam giác ABC vuông tại A, vẽ tia phân giác BD. Kẻ DE vuông góc với BC (E thuộc BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng: a) Tam giác BED bằng tam giác BAD b) Tam BCF cân tại B. c) BD là đường trung tuyến của tam giác BCF?
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
c: ΔBFC can tai B
mà BD là phân giác
nên BD là trung tuyến
Đúng 1
Bình luận (0)
BÀI 4. Cho tam giác ABC vuông tại A, phân giác BD, từ D vẽ Dh vuông góc BC (H thuộc BC). Kẻ Hd cắt BA tại E
a, Chứng minh tam giác ABH cân
b, Chứng minh BD vuông góc với Ec
Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc với BD cắt BC tại K.
a. Chứng minh: Tam giác ABK cân tại B
b. Chứng minh rằng: DK vuông góc với BC.
c. Kẻ AH vuông góc với BC. Chứng minh rằng: AK là tia phân giác của góc HAC.
d. Gọi I là giao điểm của AH và BD. Chứng minh rằng: IK // AC.
Đọc tiếp
Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc với BD cắt BC tại K.
a. Chứng minh: Tam giác ABK cân tại B
b. Chứng minh rằng: DK vuông góc với BC.
c. Kẻ AH vuông góc với BC. Chứng minh rằng: AK là tia phân giác của góc HAC.
d. Gọi I là giao điểm của AH và BD. Chứng minh rằng: IK // AC.
a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :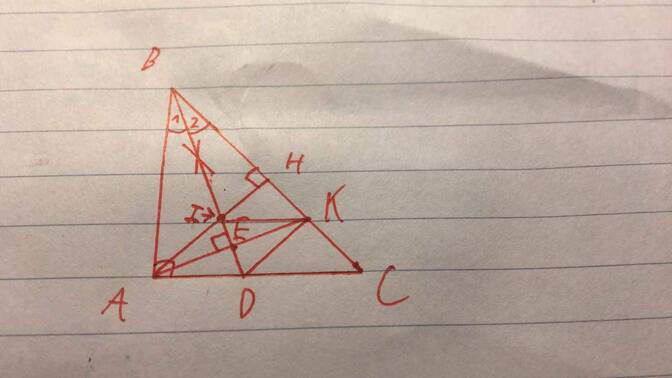
Đúng 3
Bình luận (0)
Cho tam giác ABC cân tại A .
a/ Chứng minh góc B,C luôn là góc nhọn
b/Nếu tam giác ABC có A = 100 0 . Lấy các D,E trên cạnh BC sao cho BD = BA ; CE = CA .
Chứng minh tam giác AED cân .
c/ Vẽ phân giác ngoài tại đỉnh A của tam giác ABC . Chứng minh đường phân giác này song song
với BC .
giúp mk nha cảm ơn trc ạ
Cho tam giác ABC cân tại A có 2 đường phân giác AM và BD, phân giác góc BDA cắt BC tại N. Chứng minh rằng BD=1/2MN?