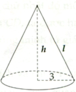
Cho hình nón bán kính đáy bằng 3 và chiều cao bằng 4. Diện tích toàn phần của hình nón đã cho bằng
![]()
![]()
![]()
![]()
Cho hình nón có bán kính đáy bằng 4a và chiều cao bằng 3a. Diện tích toàn phần của hình nón đã cho bằng
![]()
![]()
![]()
![]()
Cho hình nón có chiều cao bằng 8cm, bán kính đáy bằng 6cm. Diện tích toàn phần của hình nón đã cho bằng
![]()
![]()
Cho hình nón có chiều cao bằng 8cm, bán kính đáy bằng 6cm. Diện tích toàn phần của hình nón đã cho bằng
A. 116 πcm 3
B. 84 πcm 3
C. 96 πcm 3
D. 132 πcm 3
Chọn C.
Phương pháp:
Công thức liên hệ giữa bán kính đáy, chiều cao và đường sinh của hình nón:
![]()
Diện tích xung quanh của hình nón :
![]()
Diện tích toàn phần của hình nón :

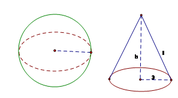
Cho hình cầu có bán kính 3cm. Một hình nón cũng có bán kính đáy bằng 3cm và có diện tích toàn phần bằng diện tích mặt cầu. Tính chiều cao của hình nón:
A. 3
B. 6 3
C. 72
D. 6 2
Đáp án D
Gọi l là độ dài đường sinh của hình nón.
Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có:
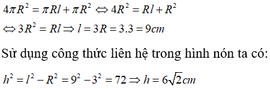
Cho hình cầu có bán kính 3cm. Một hình nón cũng có bán kính đáy bằng 3cm và có diện tích toàn phần bằng diện tích mặt cầu. Tính chiều cao của hình nón:
A. 3
B. 6 3
C. 72
D. 6 2
Đáp án D
Gọi l là độ dài đường sinh của hình nón.
Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có:
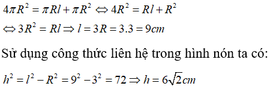
Hình nón có chiều cao bằng 4/3 bán kính đáy. Tỉ số giữa diện tích toàn phần và diện tích xung quanh của hình nón là:
A. 4/3
B. 5/7
C. 8/5
D. 9/5
Cho hình nón tròn xoay có chiều cao h, đường sinh l và bán kính đường tròn đáy bằng R. Diện tích toàn phần của hình nón bằng
![]()
![]()
![]()
![]()
Cho hình nón tròn xoay có chiều cao h, đường sinh l và bán kính đường tròn đáy bằng R. Diện tích toàn phần của hình nón bằng
A. 2 πR ( l + R )
B. πR ( l + R )
C. πR ( 2 l + R )
D. πR ( l + 2 R )
Một hình cầu có bán kính 3cm. Một hình nón cũng có bán kính đáy bằng 3cm và có diện tích toàn phần bằng diện tích mặt cầu. Tính chiều cao của hình nón