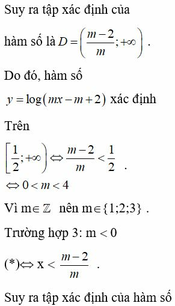Xác định tham số m để hàm số sau: y = mx - 4 x - m đồng biến trên từng khoảng xác định

Những câu hỏi liên quan
Xác định giá trị của tham số m để hàm số sau có cực trị:
y = x 3 + 2m x 2 + mx − 1
TXĐ: D = R
y’ = 3 x 2 + 4mx + m
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.
⇔ 3 x 2 + 4mx + m có hai nghiệm phân biệt.
⇔ Δ’ = 4 m 2 -3m > 0 ⇔ m(4m – 3) > 0
⇔ 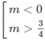
Vậy hàm số đã cho có cực đại, cực tiểu khi m < 0 hoặc m > 3/4.
Đúng 0
Bình luận (0)
Xác định giá trị của tham số m để hàm số sau có cực trị: y = x 3 + 2m x 2 + mx − 1
TXĐ: D = R
y’ = 3 x 2 + 4mx + m
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.
⇔ 3 x 2 + 4mx + m có hai nghiệm phân biệt.
⇔ ∆ ’ = 4 m 2 -3m > 0 ⇔ m(4m – 3) > 0
⇔ 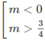
Vậy hàm số đã cho có cực đại, cực tiểu khi m < 0 hoặc m > 3/4.
Đúng 0
Bình luận (0)
y= \(\dfrac{mx}{\sqrt{x-m+2}+1}\)
a, Tìm tập xác định của hàm số theo tham số m
b, Tìm m để hàm số có tập xác định trên (0;1)
Xác định giá trị của tham số m để hàm số m để hàm số y = x 3 + m x + 1 x + m đạt giá trị cực đại tại x = 2.
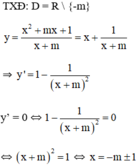
Ta có bảng biến thiên:
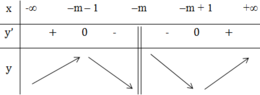
Dựa vào BBT thấy hàm số đạt cực đại tại x = -m – 1.
Hàm số đạt cực đại tại x = 2 ⇔ -m – 1 = 2 ⇔ m = -3.
Vậy m = -3.
Đúng 0
Bình luận (0)
Cho hàm số
y
m
x
+
3
x
+
m
. Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên từng khoảng xác định. A.
m
3
h
o
ặ
c
m
−
3
B.
−
2...
Đọc tiếp
Cho hàm số y = m x + 3 x + m . Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên từng khoảng xác định.
A. m > 3 h o ặ c m < − 3
B. − 2 < m < 3
C. − 2 < m < 4
D. − 3 < m < 3
Đáp án D
Ta có y ' = m 2 − 3 x + m 2 . Hàm số nghịch biến trên từng khoảng xác định
⇔ m 2 < 3 ⇔ − 3 < m < 3
Đúng 0
Bình luận (0)
Số các giá trị nguyên của tham số m để hàm số
y
log
(
m
x
-
m
-
2
)
xác định trên
[
1
2
;
+
∞
)
là:
Đọc tiếp
Số các giá trị nguyên của tham số m để hàm số y = log ( m x - m - 2 ) xác định trên [ 1 2 ; + ∞ ) là:
![]()
![]()
![]()
![]()
Có bao nhiêu giá trị nguyên của tham số m để hàm số
y
m
x
+
1
4
x
+
m
luôn nghịch biến trên từng khoảng xác định của hàm số? A. 1 B. 2 C. 3 D. vô số
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = m x + 1 4 x + m luôn nghịch biến trên từng khoảng xác định của hàm số?
A. 1
B. 2
C. 3
D. vô số
Tìm số giá trị nguyên của tham số thực m để hàm số
y
x
2
+
m
x
+
6
3
+
2
xác định trên
ℝ
. A. 9. B. 5. C. 10. D. 6.
Đọc tiếp
Tìm số giá trị nguyên của tham số thực m để hàm số y = x 2 + m x + 6 3 + 2 xác định trên ℝ .
A. 9.
B. 5.
C. 10.
D. 6.
Đáp án A
Hàm số xác định trên ℝ khi và chỉ khi
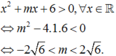
Suy ra các giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán là - 4 ; - 3 ; - 2 ; - 1 ; 0 ; 1 ; 2 ; 3 ; 4 . Vậy số 9 có giá trị nguyên tham số m .
Phân tích phương án nhiễu.
Phương án B: Sai do HS tính sai biệt thức ∆ = m 2 - 6 < 0 ⇔ - 6 < m < 6 nên tìm được 5 giá trị .
Phương án C: Sai do HS đếm sai. Cụ thể là có 5 số nguyên thuộc [ 0 ; 2 6 ) , khoảng - 2 6 ; 2 6 là khoảng đối xứng nên trong khoảng - 2 6 ; 2 6 có 10 số nguyên.
Phương án D: Sai do HS giải sai như phương án B nhưng đếm sai như phương án C.
Đúng 0
Bình luận (0)
Tìm số giá trị nguyên của tham số thực m để hàm số y = x 2 + m x + 6 3 + 2 xác định trên ℝ
A. 9
B. 5
C. 10
D. 6