Cho hàm số y = 2 2017 e 3 x - ( m - 1 ) e x + 1 . Tìm m để hàm số đồng biến trên khoảng (1;2)
A. m < 3 e 2 + 1
B. m ≥ 3 e 4 + 1
C. 3 e 3 + 1 ≤ m ≤ 3 e 4 + 1
D. 3 e 2 + 1 ≤ m ≤ 3 e 3 + 1
Những câu hỏi liên quan
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = - 2017 ( x - 1 ) ( x + 2 ) 3 ( x - 3 ) 2 Tìm số điểm cực trị của f(x)
A. 3
B. 2
C. 0
D. 1
Đáp án B
Ta có y , = 0 ⇔ x = 1 x = - 2 x = 3 , y , đổi dấu qua x=1 và x=-2 , y , không đổi dấu qua x=3 nên hàm số có hai cực trị tại x=1 và x=-2
Đúng 0
Bình luận (0)
cho hàm số y = \(\left(\frac{4}{2017}\right)^{e^{3x}-\left(m-1\right)e^x+1}\)Tìm m đểhàm số đồng biến trên (1; 2)
giải hộ :1. cho hàm số Y (27m + 15 / 32m -19 ) +2019a, tìm điều kiện để hàm số trên là hàm số bậc nhấtb, tìm m để hàm số đồng biến ,ngịch biến chú thích: dấu / là dấu chia trong phân số2.tìm điều kiện để các hàm số sau là hàm số bậc nhấta, Y(m+2 / m-3)*x+ 2b,Y(2/4x-4)*x-1c,Ycăn(2x+4)-2017d, Ycăn[(7x-2)/3m+5]*x-2015 chú thích :*2* là bình phương(vd;x bình phương)e,Y(m*2* -2m-1)*x*2*f, Y( -4m*2* -15x +19)x*2* -(2m+5)x-2017
Đọc tiếp
giải hộ :
1. cho hàm số Y = (27m + 15 / 32m -19 ) +2019
a, tìm điều kiện để hàm số trên là hàm số bậc nhất
b, tìm m để hàm số đồng biến ,ngịch biến chú thích: dấu / là dấu chia trong phân số
2.tìm điều kiện để các hàm số sau là hàm số bậc nhất
a, Y=(m+2 / m-3)*x+ 2
b,Y=(2/4x-4)*x-1
c,Y=căn(2x+4)-2017
d, Y=căn[(7x-2)/3m+5]*x-2015 chú thích :*2* là bình phương(vd;x bình phương)
e,Y=(m*2* -2m-1)*x*2*
f, Y=( -4m*2* -15x +19)x*2* -(2m+5)x-2017
Cho hàm số y = f(x) = ax4 + bx2 + c biết a > 0, c > 2017 và a + b + c < 2017. Số cực trị của hàm số y = |f(x) – 2017| là
A. 1
B. 3
C. 7
D. 5
Cho hàm số yf(x) xác định trên R và có
f
(
x
)
(
x
-
1
)
2017
(
x
2
-
1
)
(
2
x
+
3
)
3
. Hàm số yf(x) có bao nhiêu điểm cực trị? A. 1 B. 4 C. 3 D. 2
Đọc tiếp
Cho hàm số y=f(x) xác định trên R và có f ' ( x ) = ( x - 1 ) 2017 ( x 2 - 1 ) ( 2 x + 3 ) 3 . Hàm số y=f(x) có bao nhiêu điểm cực trị?
A. 1
B. 4
C. 3
D. 2
Đáp án D
f ' ( x ) = 0 ⇔ ( x - 1 ) 2017 ( x 2 - 1 ) ( 2 x + 3 ) 3 = 0 ⇔ x = 1 x = - 1 x = - 3 2
Xét dấu:
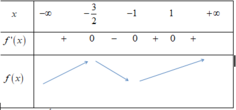
Vậy hàm số có 2 cực trị
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
v
ớ
i
a
0
,
c
2017
,
a
+
b
+
c
2017
.
Số cực trị của hàm...
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 + c v ớ i a > 0 , c > 2017 , a + b + c < 2017 . Số cực trị của hàm số y = | f ( x ) - 2017 | là
A. 1
B. 5
C. 3
D. 7
Đáp án D
Phương pháp:
+) Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017
+) Tìm số điểm cực trị của hàm số h(x) bằng cách giải phương trình h'(x) = 0
+) Xác định dấu của h(0); h(1); h(-1) và vẽ đồ thị hàm số y = h(x), từ đó vẽ đồ thị hàm số y = |h(x)| và kết luận.
Cách giải:
Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017,
với a > 0, c > 2017, a + b + c < 2017 nên b < 0
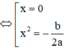
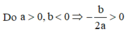
Ta có: h(0) = c - 2017 > 0, h(-1) = h(1) = a + b + c - 2017 < 0
⇒ h(0).(h-1) < 0, h(0).h(1) < 0
⇒ ∃ x1, x2: x1 ∈ (-1;0), x2 ∈ (0;1) mà h(x1) = h(x2) = 0
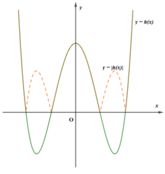
Do đó, đồ thị hàm số y = h(x) và y = |h(x)| dạng như hình vẽ bên.
Vậy, số cực trị của hàm số y = |f(x) - 2017| là 7
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
2018
ln
e
x
2018
+
e
.
Tính giá trị biểu thức
T
f
1
+
f
2
+
...
+
f
2017...
Đọc tiếp
Cho hàm số y = f x = 2018 ln e x 2018 + e . Tính giá trị biểu thức T = f ' 1 + f ' 2 + ... + f ' 2017 .
A. T = 2019 2
B. T = 1009
C. T = 2017 2
D. T = 1008
Đáp án C
Ta có: f ' x = 2018. e x 2018 + e ' e x 2018 + e = e x 2018 e x 2018 + e = g x
Lại có: g a + g 2018 − a = e a 2018 e a 2018 + e + e 1 − a 2018 e 1 − a 2018 + e = e a 2018 e a 2018 + e + e e a 2018 + e = 1
Do đó T = g 1 + g 2017 + g 2 + g 2016 + ... + g 1010 + g 1009 = 1008 + g 1009
= 1008 + 1 2 = 2017 2 .
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
2018
ln
e
x
2018
+
e
. Tính giá trị biểu thức
T
f
’
(
1
)
+
f
’
(
2
)
+
…
+
f
’
(...
Đọc tiếp
Cho hàm số y = f x = 2018 ln e x 2018 + e . Tính giá trị biểu thức T = f ’ ( 1 ) + f ’ ( 2 ) + … + f ’ ( 2017 )
A. T = 2019 2
B. T = 1009
C. T = 2017 2
D. T = 1008
Cho hàm số \(y=x^2-4x+3\) . Nếu tiếp tuyến của đồ thị hàm số tại điểm M song song với đường thẳng \(-8x+y-2017=0\) thì hoành độ \(x_o\) của M là ?
Ủa hỏi mỗi hoành độ thôi hở :D?
\(f'\left(x\right)=2x-4\)
Vi \(pttt//d:y=8x+2017\Rightarrow f'\left(x\right)=8\)
\(\Rightarrow2x-4=8\Leftrightarrow x=6\)
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm cấp hai trên R. Biết f (0)3,f (2)2018 và bẳng xét dấu của f (x) như sau: Hàm số yf(x+2017)+2018x đạt giá trị nhỏ nhất tại điểm x0 thuộc khoảng nào sau đây? A. B. C. D.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm cấp hai trên R. Biết f '(0)=3,f '(2)=2018 và bẳng xét dấu của f ''(x) như sau:
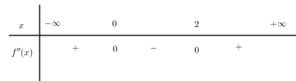
Hàm số y=f(x+2017)+2018x đạt giá trị nhỏ nhất tại điểm x0 thuộc khoảng nào sau đây?
A.
B.
C.
D.