Cho z 1 , z 2 là hai nghiệm phức của phương trình z 2 + 2 z + 2 = 0 . Giá trị của z 1 2 + z 2 2 bằng?
![]()
![]()
![]()
![]()
Số nghiệm phức của phương trình z + 2 | z | + 3 - i = ( 4 + i ) | z | z là
A. 1.
B. 2.
C. 3.
D. 4.
Kí hiệu z 1 , z 2 là hai nghiệm phức của phương trình z = 2 + 2 i Gọi M,N là các điểm biểu diễn của các số phức z 1 , z 2 Tính z = 2 + 2 i với O là gốc toạ độ.
A. T = 2 2 .
B. T = 2 2
C. T = 2 2 .
D. T = 2 2
Trong tập các số phức gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 với z 2 có phần ảo dương. Cho số phức z thỏa mãn |z- z 1 | = 1 Giá trị nhỏ nhất của P = |z- z 2 | là
A . 2016 - 1
B . 2017 - 1
C . 2017 - 1 2
D . 2016 - 1 2
Đáp án A
Phương trình 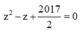
![]()
![]()
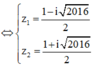
Ta có ![]()
![]()
![]()
Vật giá trị nhỏ nhất của biểu thức P là ![]()
Gọi z 1 , z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 2 = 0 . Tính | z 1 | 2 + | z 2 | 2
A. -11/9
B. 8/3
C. 2/3
D. 4/3
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 - z + 2. Tính z 1 2 + z 2 2
A. - 11 9
B. 8 3
C. 2 3
D. 4 3
trên tập hợp số phức, xét phương trình \(z^2\)-2(2m-1)z+\(m^2\)=0. Có bao nhiêu giá trị của m để phương trình có hai nghiệm phân biệt z1,z2 thỏa mãn \(z1^2\)+\(z2^2\)=2
\(z^2-2\left(2m-1\right)z+m^2=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}z_1+z_2=-\dfrac{b}{a}=2\left(2m-1\right)=4m-2\\z_1z_2=\dfrac{c}{a}=m^2\end{matrix}\right.\)
Ta có :
\(z^2_1+z_2^2=2\)
\(\Leftrightarrow\left(z_1+z_2\right)^2-2z_1z_2=2\)
\(\Leftrightarrow\left(4m-2\right)^2-2m^2-2=0\)
\(\Leftrightarrow16m^2-16m+4-2m^2-2=0\)
\(\Leftrightarrow14m^2-16m+2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m=\dfrac{1}{7}\end{matrix}\right.\)
Ta có phương trình bậc hai trên tập số phức:
z^2 - 2(2m-1)z + m^2 = 0
Theo định lý giá trị trung bình, nếu z1 và z2 là nghiệm của phương trình trên, thì ta có:
z1 + z2 = 2(2m-1) và z1z2 = m^2
Từ phương trình z1^2 + z2^2 = 2, ta suy ra:
(z1+z2)^2 - 2z1z2 = 4
Thay z1+z2 và z1z2 bằng các giá trị đã biết vào, ta được:
(2(2m-1))^2 - 2m^2 = 4
Đơn giản hóa biểu thức ta có:
m^2 - 4m + 1 = 0
Suy ra:
m = 2 + √3 hoặc m = 2 - √3
Vậy, để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, ta cần phải có m = 2 + √3 hoặc m = 2 - √3.
Kết luận: Có hai giá trị của m để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, đó là m = 2 + √3 hoặc m = 2 - √3.
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 . Giá trị nhỏ nhất của P = z - z 2 là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1
Đáp án A
Phương pháp.
Giả sử ![]() Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa
Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa ![]() về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
Lời giải chi tiết.
Tính toán ta tìm được hai nghiệm 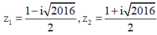
Giả sử ![]() . Từ
. Từ ![]() ta suy ra
ta suy ra
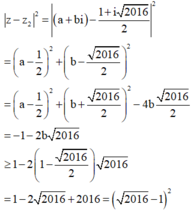
Áp dụng (1) ta nhận được
Do đó giá trị nhỏ nhất của ![]() là
2016
-
1
là
2016
-
1
Đạt được khi và chỉ khi ![]()
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 Giá trị nhỏ nhất của P = z - z 2 là
![]()
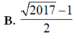
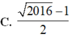
![]()
Trong tập các số phức gọi z 1 , z 2 là hai nghiệm của phương trình z 2 − z + 2017 4 = 0 với z 2 có phần ảo dương. Cho số phức z thỏa mãn z − z 1 = 1. Giá trị nhỏ nhất của P = z − z 2 là
A. 2016 − 1
B. 2017 − 1
C. 2017 − 1 2
D. 2016 − 1 2
Đáp án A
Phương trình z 2 − z + 2017 2 = 0 ⇔ 4 z 2 − 4 z + 2017 = 0
⇔ 2 z − 1 2 = 2016 i 2 ⇔ z 1 = 1 − i 2016 2 z 2 = 1 + i 2016 2
Ta có z − z 1 + z − z 2 ≥ z − z 1 − z − z 2 = z − z 2 ≥ z 1 − z 2 − z − z 1 = 2016 − 1
Vật giá trị nhỏ nhất của biểu thức P là P min = 2016 − 1
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn | z - z 1 |=1 Giá trị nhỏ nhất của P=| z - z 2 |là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1