Cho số phức z thoả mãn 2 - i z - 3 i - 1 z - i = 4 Biết tập hợp điểm biểu diễn số phức w = 1 i z + 1 là một đường tròn bán kính R. Mệnh đề nào dưới đây đúng ?
A. R = 4 .
B. R = 4 5 .
C. R = 8 .
D. R = 2 2 .
Những câu hỏi liên quan
Cho số phức z thoả mãn
2
z
+
1
2
z
-
i
2
. Tính môđun của số phức z+2+i. A.1 B.3 C.4 D.2
Đọc tiếp
Cho số phức z thoả mãn 2 z + 1 2 = z - i 2 . Tính môđun của số phức z+2+i.
A.1
B.3
C.4
D.2
Cho số phức z thoả mãn (2+z)i=3-2i. Phần thực của z bằng
A. -2.
B. -3.
C. -4.
D. -5.
Cho số phức z thoả mãn 2|z-1-i|=|z+2-3i|+2|z-4+i|. Giá trị lớn nhất của |z| bằng
A. 17
B. 13
C. 10
D. 2 5
Cho số phức Z thoả mãn (1+2i)z-5= 3i tìm số phức liên hợp z 2/ cho số phức z=a+bi(a, b thuộc R) thoả mãn 3z-5z ngan -6+10i=0 .tính a-b
\(\left(1+2i\right)z-5=3i\Leftrightarrow\left(1+2i\right)z=5+3i\)
\(\Rightarrow z=\dfrac{5+3i}{1+2i}=\dfrac{11}{5}-\dfrac{7}{5}i\)
\(\Rightarrow\overline{z}=\dfrac{11}{5}+\dfrac{7}{5}i\)
2.
Đề câu này là: \(3z-5\overline{z}-6+10i=0\) đúng không nhỉ?
Đúng 0
Bình luận (0)
Cho N là điểm biểu diễn số phức z thỏa mãn \(\dfrac{z+2-3i}{z-3}=1-i\) và M là điểm biểu diễn số phức z' thoả mãn \(\left|z'-2-i\right|+\left|z'+3-3i\right|=\sqrt{29}\). Tìm giá trị nhỏ nhất của MN
Cho số phức z = a + b i a , b ∈ ℝ thoả mãn z+3+i-|z|(2+i)=0 và |z|>1. Tính P=a+2b.
A. P = -1
B. P = 8
C. P = 7
D. P = 5
Cho số phức z thoả mãn |z-1-i|=1 Khi 3|z|=2|z-4-4i| đạt giá trị lớn nhất. Tính |z|
A. 2 - 1
B. 2
C. 2 + 1
D. 3
Đặt 
Khi đó
Dấu bằng đạt tại
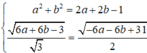
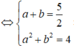
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho số phức z thoả mãn đồng thời hai điều kiện
z
-
3
-
4
i
5
và biểu thức
M
z
+
2
2
-
z
-
i
2
đ...
Đọc tiếp
Cho số phức z thoả mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = z + 2 2 - z - i 2 đạt giá trị lớn nhất. Môđun của số phức z - 2 - i bằng
A. 5
B. 9
C. 25
D. 5
Cho hai số phức z,w thoả mãn |z-1-i|=1,| w ¯ -2-3i|=2. Giá trị nhỏ nhất của |z-w| bằng
A. 13 -3.
B. 17 -3.
C. 17 +3.
D. 13 +3
Cho các số phức z_1, z_2 thoả mãn left|z-2right|left|zright| và left|z_2-z_1right|4. Số phức w thoả mãn left|w-3-5iright|1, số phức u thoả mãn left|u-4+4iright|2. Giá trị nhỏ nhất của Tleft|w-z_2right|+left|u-z_1right| làA. 5sqrt{3}-3 B. 5sqrt{2}-3 C. 2sqrt{5}-3 D. 5sqrt{3}-2
Đọc tiếp
Cho các số phức \(z_1\), \(z_2\) thoả mãn \(\left|z-2\right|=\left|z\right|\) và \(\left|z_2-z_1\right|=4\). Số phức \(w\) thoả mãn \(\left|w-3-5i\right|=1\), số phức \(u\) thoả mãn \(\left|u-4+4i\right|=2\). Giá trị nhỏ nhất của \(T=\left|w-z_2\right|+\left|u-z_1\right|\) là
A. \(5\sqrt{3}-3\) B. \(5\sqrt{2}-3\) C. \(2\sqrt{5}-3\) D. \(5\sqrt{3}-2\)