Cho hàm số f(x) thỏa mãn f ' x 2 + f ( x ) . f ' ' ( x ) = 15 x 4 + 12 x , ∀ x ∈ ℝ và f(0)=f'(0)=1. Giá trị của f 1 2 là
A. 10
B. 8
C. 5 2
D. 9 2
Cho hàm số F ( x ) = a x 3 + b x 2 + c x + 1 là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là
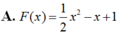
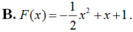
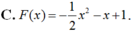
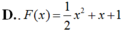
Cho hàm số f(x) thỏa mãn 2.f(1/x)+f(x)= x^2. Tính f(3)
cho hàm số f(x) thỏa mãn: (x+2)f(-x)=(1-x)f(x). Tính f(-1/2)
Cho F(x) là một nguyên hàm của hàm số f ( x ) = e x + 2 x thỏa mãn F(0)=3/2. Tìm F(x)
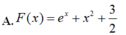
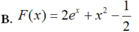
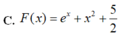
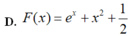
Cho hàm số y = f ( x ) thỏa mãn f ( 2 ) = 1 4 và f ' ( x ) = 2 x . [ f ( x ) ] 2 với ∀ x ∈ R tính f ( 1 )
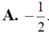
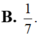
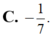
![]()
Cho hàm số f(x) thỏa mãn f ' ( x ) = ( x + 1 ) e x và f(0)=1. Tính f(2)
A. f ( 2 ) = 4 e 2 + 1
B. f ( 2 ) = 2 e 2 + 1
C. f ( 2 ) = 3 e 2 + 1
D. f ( 2 ) = e 2 + 1
Cho hàm số f ( x ) = 2 x + e x . Tìm một nguyên hàm F(x) của hàm số f(x) thỏa mãn F(0)=2019
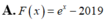
![]()
![]()
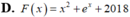
Cho hàm số f ( x ) thỏa mãn f ' ( x ) = x e x và f ( 0 ) = 2 Tính f ( 1 ) .
![]()
![]()
![]()
![]()
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 x - 1 thỏa mãn F(5)=2 và F(0)=1. Tính F(2)-F(-1)
A. 1+ln2
B. 0
C. 1-3ln2
D. 2+ln2
Chọn đáp án C
Phương pháp
Sử dụng công thức nguyên hàm:
![]()
dựa dữ kiện đề bài tìm được C, từ đó tính F(2)-F(-1)
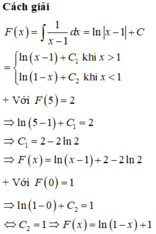

Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 x - 1 thỏa mãn F(5)=2 và F(0)=1. Tính F(2)-F(-1).
![]()
![]()
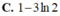
![]()