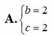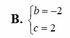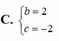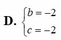Tìm số phức z là nghiệm chung của hai phương trình: iz + 1 = 0 và z 4 - 1 = 0
A. z = 1
B. z = -1
C. z = i
D. Không tồn tại
Cho số phức z có phần ảo là số âm và là nghiệm của phương trình z − 2 2 + z 2 = 0 . Môđun của số phức w = i z + 2 z là
A. 2
B. 2 2
C. 2
D. 4
Cho số phức z có phần ảo là số âm và là nghiệm của phương trình z − 2 2 + z 2 = 0. Môđun của số phức w = i z + 2 z là
A. 2
B. 2 2
C. 2
D. 4
Gọi z1; z2 là hai nghiệm phức của phương trình z2 – z + 1 = 0 . Tìm phần thực, phần ảo của số phức ![]() lần lượt là?
lần lượt là?
A. 0; 1
B. 1; 0
C. -1; 0
D. 0; -1
Chọn C.
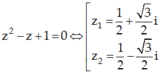
Ta có 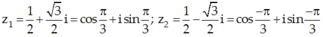
Áp dụng công thức Moa-vrơ:
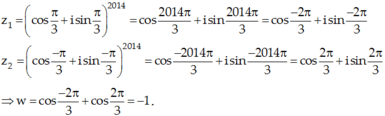
Phần thực của w là -1, phần ảo là 0.
Tìm số phức Z, biết Z là nghiệm của phương trình: ( 2 i - 1 ) Z 2 - 2 i Z ¯ + ( 6 + 4 i ) = 0
A. Z = -i
B. Z = 1-i
C. Z = 1+i
D. Z = i
Phương trình z + i z + i 2 . . . z + i 10 = 0 có bao nhiêu nghiệm phức?
A. Có 10 nghiệm
B. Có 4 nghiệm
C. Có 3 nghiệm
D. Có 2 nghiệm
Phương trình z 2 + b z + c = 0 có một nghiệm phức là z = 1 - 2 i .Tích của hai số b và c bằng
A. 3
B.-10
C.-2 và 5
D. 5
Phương trình z 2 + b z + c = 0 có một nghiệm phức là z = 1 - 2i. Tích của hai số b và c bằng:
A. 3
B. -10
C. -2 và 5
D. 5
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Chọn D.
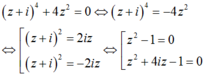
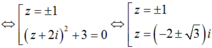
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Tìm hai số thực b và c biết rằng phương trình z 2 + b z + c = 0 có nghiệm phức z = 1+i