Cho mặt cầu (S): x 2 + y 2 + z 2 - 2x + 4y - 2z - 3 = 0 cắt 2 mặt phẳng (P): x - 2y + z = 0 và (Q): x - z - 2 = 0 theo các đường tròn giao tuyến với bán kính r 1 ; r 2 . Khi đó tỉ số r 1 r 2 bằng
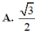
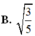
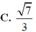
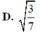
Cho mặt cầu S : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z - 3 = 0 cắt 2 mặt phẳng P : x - 2 y + z = 0 và Q : x - z - 2 = 0 theo các đường tròn giao tuyến với bán kính r 1 , r 2 . Khi đó tỉ số r 1 r 2 bằng
A. 3 2
B. 3 5
C. 7 3
D. 3 7
Đáp án D
Mặt cầu (S) có tâm I(1;-2;1), bán kính R = 3
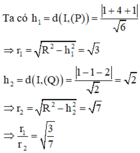
Trong không gian tọa độ Oxyz, cho mặt cầu (S): ( x - 2 ) 2 + y 2 + ( z + 1 ) 2 = 9 và mặt phẳng (P): 2x-y-2z-3=0. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn (C). Tính bán kính R của (C)
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxyz, cho mặt cầu (S): (x-2)2 + y2 + (z+1)2 = 9 và mặt phẳng (P): 2x-y-2z-3=0. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn (C). Tính bán kính R của (C).
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + z2 - 2x + 4y - 4z -16 = 0 và mặt phẳng (P): x + 2y - 2z - 2 = 0. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính là:
A. r = 6
B. r = 2 2
C. r = 4
D. r = 2 3
Chọn C
Mặt cầu (S): x2 + y2 + z2 - 2x + 4y - 4z -16 = 0 có tâm I (1; -2; 2) bán kính R = 5
Khoảng cách từ I (1; -2; 2) đến mặt phẳng (P): x + 2y - 2z - 2 = 0 là 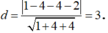
Mặt phẳng cắt mặt cầu theo giao tuyến là một đường tròn có bán kính là: ![]()
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x + y -2z + m = 0 và mặt cầu (S): x2 + y2 + z2 - 2x + 4y -6z - 2= 0. Có bao nhiêu giá trị nguyên của m để mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (T) có chu vi bằng 4π√3
A. 3
B. 4
C. 2
D. 1
Chọn C
(S) có tâm I (1; -2; 3) và bán kính R = 4
Gọi H là hình chiếu của I lên (P).
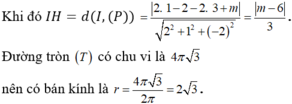
(P) cắt mặt cầu (S) theo giao tuyến là đường tròn (T) có chu vi bằng 4π√3
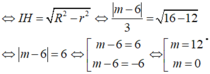
Vậy có 2 giá trị nguyên của m thỏa mãn.
Trong không gian Oxyz, cho mặt cầu \(\left(S\right):x^2+y^2+z^2-2x+4y+2z-19=0\) và mặt phẳng \(\left(P\right):x-2y+2z-12=0\)
a) Chứng minh rằng (P) cắt (S) theo một đường tròn
b) Tìm tọa đọ tâm và bán kính của đường tròn đó
Trong không gian với hệ trục tọa độ Oxyz cho mặt cầu S : x 2 + y 2 + z 2 - 6 x - 4 y - 12 z = 0 và mặt phẳng P : 2 x + y - z - 2 = 0 . Tính diện tích thiết diện của mặt cầu (S) cắt bởi mặt phẳng (P).
A. S = 49 π
B. S = 50 π
C. S = 25 π
D. S = 36 π
trong không gian tọa độ oxyz , cho mặt cầu (s) : (x-2)^2+y^2+(z+1)^2=9 và mặt phẳng (P) : 2x-y-2z-3=0. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đtròn (C) . Tính bán kính R của (C)
giúp mình vs ạ . mình cảm ơn
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 6x + 3y -1 =0 và mặt cầu (S): x2 + y2 + z2 -6x -4y -2z -11 =0. Chứng minh mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn (C). Tìm tọa độ tâm của (C).