Trong không gian Oxyz, cho véc tơ a → biểu diễn của các véc tơ đơn vị là a → = 2 i → + k → − 3 j → . Tọa độ của véc tơ a → là:
A. 1 ; 2 ; − 3
B. 2 ; − 3 ; 1
C. 2 ; 1 ; − 3
D. 1 ; − 3 ; 2
Trong không gian Oxyz, cho véc tơ a → biểu diễn của các véc tơ đơn vị là a → = 2 i → + k → - 3 j → . Tọa độ của véc tơ a → là:
A. (1;2;-3)
B. (2;-3;1)
C. (2;1;-3)
D. (1;-3;2)
Trong không gian với hệ tọa độ Oxyz, cho véc-tơ ![]() =(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ
=(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ ![]() ?
?
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxyz, cho đường thẳng d: ![]() .Véc tơ nào trong các véc tơ sau đây không là véc tơ chỉ phương của đường thẳng d?
.Véc tơ nào trong các véc tơ sau đây không là véc tơ chỉ phương của đường thẳng d?
A. u 1 → = 2 ; - 2 ; 2
B. u 1 → = - 3 ; 3 ; - 3
C. u 1 → = 4 ; - 4 ; 4
D. u 1 → = 1 ; 1 ; 1
Đáp án D
Phương pháp:
Đường thẳng d: 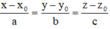 có 1 VTCP là
có 1 VTCP là ![]() . Mọi vectơ
v
→
=
k
u
→
(
k
∈
Z
)
cùng phương với vecto
u
→
đều là VTCP của đường thẳng d
. Mọi vectơ
v
→
=
k
u
→
(
k
∈
Z
)
cùng phương với vecto
u
→
đều là VTCP của đường thẳng d
Cách giải: Đường thẳng d nhận u 1 → = 1 ; - 1 ; 1 là 1 VTCP. Mọi vecto cùng phương với vecto đều u → là VTCP của đường thẳng d.
Ta thấy chỉ có đáp án D, vecto u 1 → = 1 ; 1 ; 1 không cùng phương với u 1 → = 1 ; - 1 ; 1 nên u 1 → = 1 ; 1 ; 1 không là VTCP của đường thẳng d
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 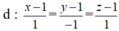 . Véc-tơ nào trong các véc-tơ sau đây không là véc-tơ chỉ phương của đường thẳng d?
. Véc-tơ nào trong các véc-tơ sau đây không là véc-tơ chỉ phương của đường thẳng d?
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x - 2y + 3z + 3 = 0. Trong các véc tơ sau véc tơ nào là véc tơ pháp tuyến của (P)?
A. n → = 1 ; 2 ; - 3
B. n → = - 1 ; 2 ; 3
C. n → = 1 ; 2 ; 3
D. n → = 1 ; - 2 ; 3
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x - 2y + 3z +3 = 0. Trong các véc tơ sau véc tơ nào là véc tơ pháp tuyến của (P)?
A. n → = ( 1 ; 2 ; - 3 )
B. n → = ( - 1 ; 2 ; 3 )
C. n → = ( 1 ; 2 ; 3 )
D. n → = ( 1 ; - 2 ; 3 )
Trong không gian tọa độ Oxyz, cho đường thẳng d : x - 1 1 = y - 1 - 1 = z - 1 1 Véc tơ nào trong các véc tơ sau đây không là véc tơ chỉ phương của đường thẳng d?
A. u 1 → =(-2;2;-2)
B. u 1 → =(-3;3;-3)
C. u 1 → =(2;-4;4)
D. u 1 → =(1;1;1)
Đáp án D
Phương pháp:
Đường thẳng
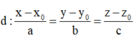
có 1 VTCP là u 1 → =(a;b;c). Mọi vectơ v → =k u → (k ∈ Z)cùng phương với vecto u → đều là VTCP của đường thẳng d.
Cách giải: Đường thẳng d nhận u → =(1;-1;1) là 1 VTCP. Mọi vecto cùng phương với vecto đều là VTCP của đường thẳng d.
Ta thấychỉ có đáp án D, vecto u 1 → =(1;1;1) không cùng phương với u → =(1;-1;1) nên u 1 → =(1;1;1) không là VTCP của đường thẳng d.
Trong không gian Oxyz, cho hai véc tơ a → = − 4 ; 5 ; − 3 và b → = 2 ; − 2 ; 3 .
.Véc tơ x → = a → + 2 b → có tọa độ là
A. − 2 ; 3 ; 0
B. 0 ; 1 ; − 1
C. 0 ; 1 ; 3
D. − 6 ; 8 ; − 3
C
a → = − 4 ; 5 ; − 3 , b → = 2 ; − 2 ; 3
⇒ 2 b → = 4 ; − 4 ; 6
Có x → = a → + 2 b → suy ra tọa độ của vectơ x → = 0 ; 1 ; 3
Trong không gian với hệ trục Oxyz, cho 2 điểm A ( 2 ; 1 ; − 3 ) ; B ( 2 ; 4 ; 1 ) . Gọi (d) là đường thẳng đi qua trọng tâm tam giác ABO sao cho tổng khoảng cách từ các điểm A, B, O đến đường thẳng (d) là lớn nhất. Trong các véc tơ sau, véc tơ nào là một véc tơ chỉ phương của (d)?
A. u → = 13 ; 8 ; 6
B. u → = − 13 ; 8 ; 6
C. u → = 13 ; 8 ; − 6
D. u → = − 13 ; 8 ; − 6
Đáp án D
Điểm A ( 2 ; 1 ; − 3 ) , B ( 2 ; 4 ; 1 ) , O 0 ; 0 ; 0 suy ra G là trọng tâm tam giác ABO là G 2 3 ; 5 3 ; − 2 3
Gọi M, N, P lần lượt là hình chiếu vuống góc cuả A, B, O trên đường thẳng d
Khi đó, khoảng cách:
d A → d = A M ; d B → d = B N ; d O → d = O P
Mặt khác A M ≤ A G B N ≤ B G O P ≤ O G
⇒ d A → d + d B → d + d O → d ≤ A G + B G + O G = c o n s t
Dấu “=” xảy ra khi và chỉ khi đường thẳng d vuông góc mặt phẳng A B O tại G
Ta có O A → = 2 ; 1 ; − 3 O B → = 2 ; 4 ; 1 ⇒ n A B O → = 13 ; − 8 ; 6
⇒ véc tơ chỉ phương của (d) là u → = − 13 ; 8 ; − 6