Cho hình chóp S.ABCD có đáy là hình thang vuông tại A,B Biết S A ⊥ A B C D , A B = B C = a , A D = 2 a , S A = a 2 . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm S , A , B , C , E .
A. a 30 6
B. a 6 6
C. a 3 2
D. a
Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB a, cạnh đáy CD 2a, AD a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng
3
a
2
2
. Thể tích của hình chóp S.ABCD bằng:A.
a
3
B.
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết ABa, BC2a, BDa
10
. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là
60
0
. Tính thể tích V của khối chóp S.ABCD theo a.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB=a, BC=2a, BD=a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 60 0 . Tính thể tích V của khối chóp S.ABCD theo a.
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB a, BC 2a, BD a
10
. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a A.
V
3
30
a...
Đọc tiếp
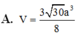
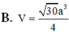
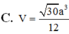
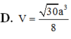
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
Đáp án D
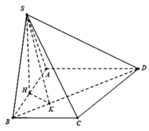
Dựng HK ⊥ BD, do SH ⊥ BD nên ta có:
(SKH) ⊥ BD => Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là góc SKH = 600
Lại có: 
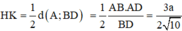
Do đó 
Vậy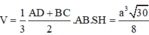 
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB a, BC 2a, BD a
10
. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a. A. V
3
30
a
3
8
B. V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a.
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
Chọn D
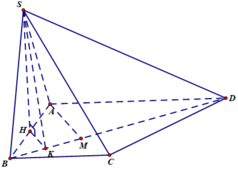
Ta có 
Gọi H là trung điểm AB thì 
,
kẻ 
, ta có 
là góc giữa (SBD) và (ABCD), do đó 
= 600
Gọi AM là đường cao của tam giác vuông ABD. Khi đó, ta có:
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB a, BC 2a,
B
D
a
10
. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 60 độ. Tính thể tích V của khối chóp S.ABCD theo a. A.
V
3
30
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB =a, BC =2a, B D = a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 60 độ. Tính thể tích V của khối chóp S.ABCD theo a.
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết
A
B
a
,
B
C
2
a
,
B
D
a
10
Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là
60
°
. Tính thể tích V của khối chóp S.ABCD theo a. A.
V...
Đọc tiếp
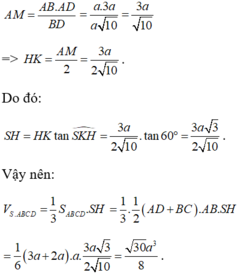
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết A B = a , B C = 2 a , B D = a 10 Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 60 ° . Tính thể tích V của khối chóp S.ABCD theo a.
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B; Biết SA vuông góc với mặt đáy, SA
a
2
Tính theo a khoảng cách d từ B đến mặt phẳng (SCD)
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B; 
Biết SA vuông góc với mặt đáy, SA=
a
2
Tính theo a khoảng cách d từ B đến mặt phẳng (SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, AD DC a, AB 2a (a 0). Hình chiếu của S lên mặt đáy trùng với trung điểm I của AD. Thể tích khối chóp S.IBC biết góc giữa SC và mặt đáy bằng
60
0
A
.
a
3
5
24
B
.
a...
Đọc tiếp
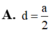
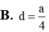
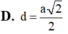
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, AD = DC = a, AB = 2a (a > 0). Hình chiếu của S lên mặt đáy trùng với trung điểm I của AD. Thể tích khối chóp S.IBC biết góc giữa SC và mặt đáy bằng 60 0
A . a 3 5 24
B . a 3 15 24
C . a 3 5 8
D . a 3 15 8
Đáp án D
Vì I là hình chiếu của S trên (ABCD)
=
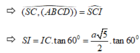a
15
2
Vậy 
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A , D , AD DC a , AB 2a (a 0) Hình chiếu của S lên mặt đáy trùng với trung điểm I của AD. Thể tích khối chóp S.IBC biết góc giữa SC và mặt đáy bằng
60
°
A.
m
-
3
B.
m
-
1
2
C.
m
1
2
D.
m...
Đọc tiếp
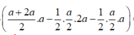
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A , D , AD = DC = a , AB = 2a (a > 0) Hình chiếu của S lên mặt đáy trùng với trung điểm I của AD. Thể tích khối chóp S.IBC biết góc giữa SC và mặt đáy bằng 60 °
A. m = - 3
B. m = - 1 2
C. m = 1 2
D. m = 1
Đáp ván A
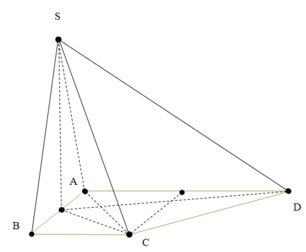
Vì I là hình chiếu của S trên (ABCD)
⇒ ( S C → , ( A B C D ) ) = S C I ⏞
⇒ S I = I C . tan 60 ° = a 5 2 . tan 60 ° = a 15 2
Vậy
V S . I B C = V S . A B C D - V S . A I B - V S . I C D = 1 3 . a 15 2 a + 2 a 2 . a - 1 2 . a 2 . 2 a - 1 2 . a 2 . a = a 3 15 8
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A, B. Biết
S
A
⊥
A
B
C
D
,
A
B
B
C
a
,
A
D
2
a
,
S
A
a
2
. Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điể...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A, B. Biết S A ⊥ A B C D , A B = B C = a , A D = 2 a , S A = a 2 . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm S, A, B, C, E
A. a
B. a 6 3
C. a 3 2
D. a 30 6
