Cho hàm số y = 0,2 x 2 và y = x.
Vẽ hai đồ thị của những hàm số này trên cùng một mặt phẳng tọa độ.
Cho hai hàm số y = 1 3 x 2 và y = -x + 6.
a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị đó.
a)
- Vẽ đường thẳng y = -x + 6
Cho x = 0 ⇒ y = 6 được điểm (0, 6)
Cho y = 0 ⇒ x = 6 được điểm (6, 0)
⇒ Đường thẳng y = -x + 6 đi qua các điểm (6; 0) và (0; 6).
- Lập bảng giá trị và vẽ đồ thị hàm số 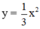
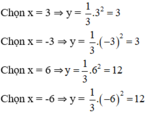
⇒ Parabol đi qua các điểm (3; 3); (-3; 3); (-6; 12); (6; 12); (0; 0).
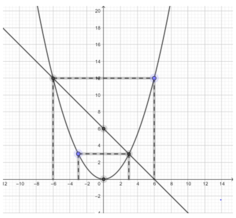
b)Xét phương trình hoành độ giao điểm

Cho hai hàm số \(y=0,2x^2\) và \(y=x\)
a) Vẽ hai đồ thị của những hàm số này trên cùng một mặt phẳng tọa độ ?
b) Tìm tọa độ của những giao điểm của hai đồ thị ?
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}0,2x^2-x=0\\y=x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(0,2x-1\right)=0\\y=x\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;1\right);\left(5;5\right)\right\}\)
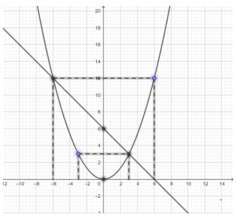
Cho hai hàm số y = 1 3 x 2 và y = -x + 6.
Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.
- Vẽ đường thẳng y = -x + 6
Cho x = 0 ⇒ y = 6 được điểm (0, 6)
Cho y = 0 ⇒ x = 6 được điểm (6, 0)
⇒ Đường thẳng y = -x + 6 đi qua các điểm (6; 0) và (0; 6).
- Lập bảng giá trị và vẽ đồ thị hàm số 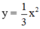
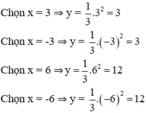
⇒ Parabol đi qua các điểm (3; 3); (-3; 3); (-6; 12); (6; 12); (0; 0).
cho hàm số : y=x\(^2\)và y=-2x+3
a) vẽ đồ thị của hàm số trên cùng mặt phẳng tọa độ Oxy.
b) tìm tọa độ các giao điểm của hai đồ thị trên
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2=-2x+3\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+2x-3=0\\y=x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+3\right)\left(x-1\right)=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(-3;9\right);\left(1;1\right)\right\}\)
Cho hàm số \(y=\dfrac{1}{2}x^2\) có đồ thị thì (P) và đường thẳng (d) có phương trình: \(y=x+1\)
a, Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ Oxy
b, Tìm tọa độ giao điểm của 2 hàm số trên.
Cho hàm số y = ax2a) Xác định a để đồ thị của hàm số trên đi qua điểm A (4 ; 4).
b) Vẽ đồ thị của hàm số trên với a vừa tìm được và đồ thị của hàm số y = \(-\dfrac{1}{2}x\) trên cùng một mặt phẳng tọa độ Oxy.
c) Tìm tọa độ giao điểm của hai hàm số trên (câu b) bằng phép toán.
a) Để đồ thị hàm số \(y=ax^2\) đi qua điểm A(4;4) thì
Thay x=4 và y=4 vào hàm số \(y=ax^2\), ta được:
\(a\cdot4^2=4\)
\(\Leftrightarrow a\cdot16=4\)
hay \(a=\dfrac{1}{4}\)
a, - Thay tọa độ điểm A vào hàm số ta được : \(4^2.a=4\)
\(\Rightarrow a=\dfrac{1}{4}\)
b, Thay a vào hàm số ta được : \(y=\dfrac{1}{4}x^2\)
- Ta có đồ thì của hai hàm số :
c, - Xét phương trình hoành độ giao điểm :\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy hai hàm số trên cắt nhau tại hai điểm : \(\left(0;0\right);\left(-2;1\right)\)
Cho hai hàm số y=1/4 x² và y=x-1
a) biểu diễn đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ
b) tìm tọa độ giao điểm của hai đồ thị
\(a,y=\dfrac{1}{4}x^2\)
Cho \(x=1=>y=\dfrac{1}{4}\\ x=2=>y=1\\ x=3=>y=\dfrac{9}{4}\\ x=4=>y=4\\ x=5=>y=\dfrac{25}{4}\)
Vẽ đồ thị đi qua các điểm \(\left(1;\dfrac{1}{4}\right);\left(2;1\right);\left(3;\dfrac{9}{4}\right);\left(4;4\right);\left(2;\dfrac{25}{4}\right)\)
\(y=x-1\)
\(Cho\) \(x=0=>y=-1\) ta được điểm \(\left(0;-1\right)\)
Cho \(y=0=>x=1\) ta được điểm \(\left(1;0\right)\)
Vẽ đồ thị đi qua hai điểm \(\left(0;-1\right);\left(1;0\right)\)
b, Hoành độ giao điểm của hai hàm số là nghiệm của pt
\(\dfrac{1}{4}x^2=x-1\\ < =>\dfrac{1}{4}x^2-x+1=0\\ < =>x=2\)
Thay \(x=2\) vào \(y=x-1\)
\(\Leftrightarrow y=2-1=1\)
Vậy tọa độ giao điểm là \(\left(2;1\right)\)
Lời giải:
a. Bạn có thể tự vẽ
b. PT hoành độ giao điểm: $\frac{1}{4}x^2=x-1$
$\Leftrightarrow x^2=4(x-1)$
$\Leftrightarrow x^2-4x+4=0$
$\Leftrightarrow (x-2)^2=0\Leftrightarrow x=2$
Với $x=2$ thì $y=x-1=2-1=1$
Vậy tọa độ giao điểm của 2 đths là $(2,1)$
Cho hai hàm số bậc nhất y = x và y = - x + 2 có đồ thị lần lượt là (d) và (d’)
a/ Hàm số nào là hàm số nghịch biến trên R? Vì sao?
b/ Vẽ hai đồ thị hàm số trên cùng một mặt phẳng tọa độ. Tìm tọa độ giao điểm của hai đồ thị trên bằng phép tính
c/ Cho đường thẳng (d’’): y = (m-1)x + 2m. Tìm m để (d), (d’)
Và (d’’) đồng quy.
\(a,-1< 0\Leftrightarrow\left(d'\right)\text{ nghịch biến trên }R\\ b,\text{PT hoành độ giao điểm: }x=-x+2\Leftrightarrow x=1\Leftrightarrow y=1\Leftrightarrow A\left(1;1\right)\\ \text{Vậy }A\left(1;1\right)\text{ là giao 2 đths}\\ c,\text{3 đt đồng quy }\Leftrightarrow A\left(1;1\right)\in\left(d''\right)\\ \Leftrightarrow m-1+2m=1\\ \Leftrightarrow3m=2\Leftrightarrow m=\dfrac{2}{3}\)
Cho hai hàm số y = \(\dfrac{1}{2}x^2\) và y = x2.
a.Vẽ đồ thị của hai hàm số này trên cùng mặt phẳng tọa độ .
b.Tìm tọa độ hai điểm A ; B có cùng hoành độ x = 2 theo thứ tự nằm trên hai đồ thị .
c.Gọi A’ và B’ lần lượt là các điểm đối xứng với A ; B qua trục tung Oy . Kiểm tra xem A’ ; B’ có lần lượt nằm trên hai đồ thị đó không ?
a: 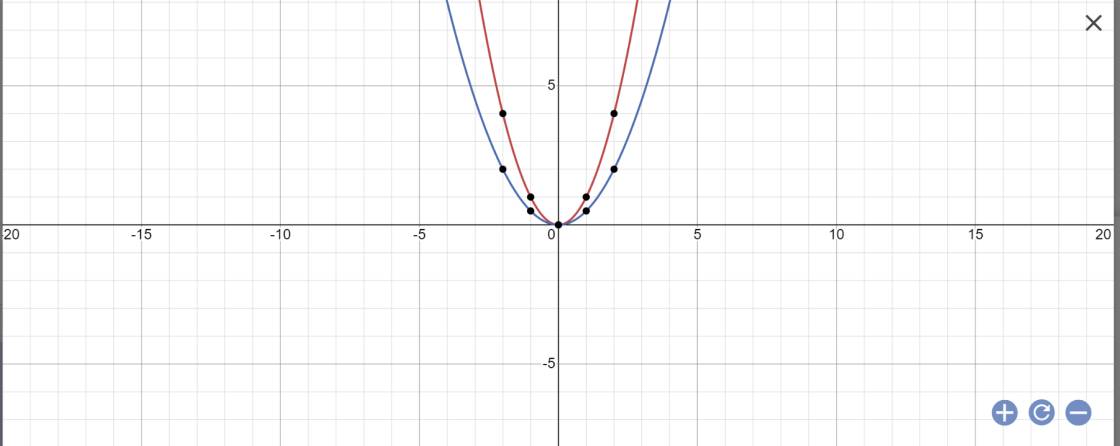
b: Khi x=2 thì y=1/2*2^2=2
=>A(2;2)
Khi x=2 thì y=2^2=4
=>B(2;4)
c: Tọa độ A' là:
\(\left\{{}\begin{matrix}x_{A'}=-x_A=-2\\y_{A'}=y_A=2\end{matrix}\right.\)
Vì f(-2)=1/2*(-2)^2=2
nên A' thuộc (P1)
Tọa độ B' là:
\(\left\{{}\begin{matrix}x_{B'}=-x_B=-2\\y_{B'}=y_B=4\end{matrix}\right.\)
Vì f1(-2)=(-2)^2=4
nên B' thuộc y=x^2