Tìm bán kính mặt cầu ngoại tiếp tứ diện ABCD với A(3;3;0); B(3;0;3); C(0;3;3) và D(3;3;3)
Những câu hỏi liên quan
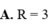
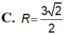
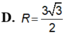
Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD với AB=2a
Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC) và AD a, AC 2a. cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD. A.
r
a
5
B.
r
a
3
2
C. r a D.
r
a
5
2
Đọc tiếp
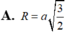
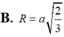
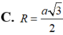
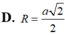
Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC) và AD = a, AC = 2a. cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.
A. r = a 5
B. r = a 3 2
C. r = a
D. r = a 5 2
Cho tứ diện
A
B
C
D
có DA vuông góc với mặt phẳng
(
A
B
C
)
và
A
D
a
,
A
C
2
a
, cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện
A
B
C
D
.
Đọc tiếp
Cho tứ diện A B C D có DA vuông góc với mặt phẳng ( A B C ) và A D = a , A C = 2 a , cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện A B C D .
Tính bán kính R mặt cầu ngoại tiếp tứ diện đều ABCD cạnh a
2
Đọc tiếp
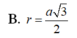
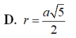
Tính bán kính R mặt cầu ngoại tiếp tứ diện đều ABCD cạnh a 2
Cho tứ diện ABCD có tam giác BCD vuông tại B, AC vuông góc với mặt phẳng (BCD). Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD
Đọc tiếp
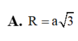
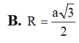
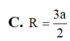
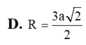
Cho tứ diện ABCD có tam giác BCD vuông tại B, AC vuông góc với mặt phẳng (BCD). Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD
Cho tứ diện ABCD có DA vuông góc với (ABC) và AD a, AC 2a; cạnh BC vuông góc với cạnh AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD. A.
r
a
5
B.
r
a
3
2
C. r a D.
r
a
5
2
Đọc tiếp
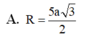
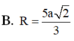
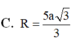
Cho tứ diện ABCD có DA vuông góc với (ABC) và AD = a, AC = 2a; cạnh BC vuông góc với cạnh AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.
A. r = a 5
B. r = a 3 2
C. r = a
D. r = a 5 2
Đáp án D
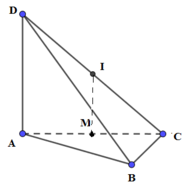
Phương pháp:
+) Xác định tâm mặt cầu ngoại tiếp khối tứ diện là điểm cách đều tất cả các đỉnh của tứ diện.
+) Áp dụng định lí Pytago tính bán kính mặt cầu ngoại tiếp tứ diện.
Cách giải:
Tam giác ABC vuông tại B, M là trung điểm của AC ⇒ M là tâm đường tròn ngoại tiếp tam giác ABC
Gọi I là trung điểm của CD ⇒ IC = ID(1)
Ta có: IM là đường trung bình của tam giác ACD ⇒ IM // AD
Mà AD ⊥ (ABC) ⇒ IM ⊥ (ABC)
Do đó, IM là trục đường tròn ngoại tiếp tam giác ABC
⇒ IA = IB = IC(2)
Từ (1), (2) ⇒ IA = IB = IC = ID ⇒ I là tâm mặt cầu ngoại tiếp tứ diện ABCD, bán kính mặt cầu:
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (BCD) vuông góc với nhai. Biết tam giác ABC đêì cạnh a, tam giá BCD vuông cân tại D. Bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng
A
.
a
2
3
B
.
a
3
3
C
.
2...
Đọc tiếp
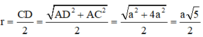
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (BCD) vuông góc với nhai. Biết tam giác ABC đêì cạnh a, tam giá BCD vuông cân tại D. Bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng
A . a 2 3
B . a 3 3
C . 2 a 3 3
D . a 3 2
Cho tứ diện ABCD có BCa, CDa
3
,
B
C
D
^
A
B
C
^
A
D
C
^
90
°
. Góc giữa đường thẳng AD và BC bằng 60...
Đọc tiếp
Cho tứ diện ABCD có BC=a, CD=a 3 , B C D ^ = A B C ^ = A D C ^ = 90 ° . Góc giữa đường thẳng AD và BC bằng 60 ° . Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD.
Tính bán kính R mặt cầu ngoại tiếp tứ diện đều ABCD cạnh
a
2
A.
R
a
3
B.
R
a
3
2
C.
R
3
a
2
D.
R
3...
Đọc tiếp
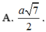
Tính bán kính R mặt cầu ngoại tiếp tứ diện đều ABCD cạnh a 2
A. R = a 3
B. R = a 3 2
C. R = 3 a 2
D. R = 3 a 2 2
Đáp án B
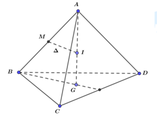
Gọi G là trọng tâm Δ B C D , ta có A G ⊥ B C D nên AG là trục của Δ B C D ,
Gọi M là trung điểm của AB. Qua M dựng đường thẳng Δ ⊥ A B , gọi I = Δ ∩ A G
Do đó mặt cầu ngoại tiếp tứ diện ABCD có tâm là I và bán kính R = I A
Ta có Δ A M I , Δ A G B là hai tam giác vuông đồng dạng nên I A A B = A M A G ⇒ A I = A B . A M A G
Do A B = a 2 , A M = a 2 2 , A G = a 2 2 − 2 3 . a 2 . 3 2 2 = 2 a 3 3
Khi đó R = A I = a 2 . a 2 2 2 a 3 3 = a 3 2
Cách 2: Áp sụng công thức giải nhanh R = A B 2 2 S G = a 3 2
Đúng 0
Bình luận (0)