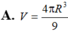
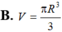
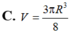
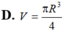
Hình nón nội tiếp trong mặt cầu bán kính R. Biết góc ở đỉnh hình nón bằng 1200. Tính thể tích V của hình nón theo R
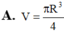
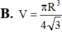
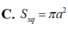
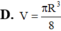
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một nón tròn xoay (N) có góc ở đỉnh bằng 60 ° . Tính tỉ số thể tích của hình trụ (T) và hình nón (N).
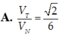
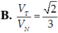
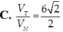
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 ° . Tính tỉ số thể tích của hình trụ (N) và hình nón (T).
A. V T V N = 2 6
B. V T V N = 2 3
C. V T V N = 3 2
D. Đáp án khác
Đáp án A.
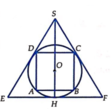
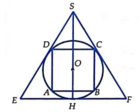
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ S E F đều” (hình vẽ).
Hình vuông ABCD nội tiếp đường tròn (O) nên
A B = B D = 2 R = A B 2 ⇔ A B = 2 R .
⇒ Bán kính đáy và chiều cao của hình trụ (T) lần lượt là r = A B 2 = 2 R 2 và h = A B = 2 R .
Thể tích khối trụ là V T = πr 2 h = π . 2 R 2 2 . 2 R = π 2 R 3 2 .
Ta có ∆ S E F đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của Δ S E F .
Gọi H là trung điểm của EF thì S H = 3 O H = 3 R ⇒ H F = S H . tan 30 ° = R 3
⇒ Bán kính đáy và chiều cao của hình nón (N) lần lượt là H F = R 3 và S H = 3 R . Thể tích khối nón là V N = 1 3 π . HF 2 . SH = 1 3 π R 3 2 . 3 R = 3 πR 3 .
Vậy V T V N = π 2 R 3 2 3 πR 3 = 2 6 .
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 0 . Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
A . V T V N = 2 6
B . V T V N = 2 3
C . V T V N = 3 2
D. Đáp án khác
Đáp án A.
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ SEF đều” (hình vẽ).
=>Bán kính đáy và chiều cao của hình trụ (T) lần lượt là
và 
Thể tích khối trụ là
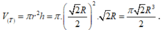
Ta có ∆ SEF đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của ∆ SEF.
Gọi H là trung điểm của EF thì
Hình vuông ABCD nội tiếp đường tròn (O) nên SH = 3OH = 3R
Bán kính đáy và chiều cao của hình nón (N) lần lượt là 
Thể tích khối nón là
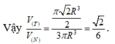
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 ° . Tính tỉ số thể tích của hình trụ (N) và hình nón (T).
A. V T V N = 2 6
B. V T V N = 2 3
C. V T V N = 3 2
D. Đáp án khác
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó. Thể tích của khối nón theo r và h.
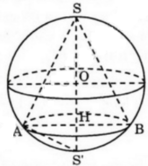
Gọi H là tâm mặt đáy của hình nón, O là tâm mặt cầu (S), đường thẳng IH cắt mặt cầu (S) tại điểm K.
Hình nón tròn xoay nội tiếp trong mặt cầu bán kính R = 3 4 có thể tích lớn nhất bằng bao nhiêu V m a x
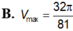
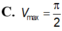
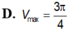
Cho hình nón tròn xoay (H) đỉnh S, đáy là hình tròn bán kính R, chiều cao bằng h. Gọi (H') là hình trụ tròn xoay có đáy là hình tròn bán kính r (0 < r < R) nội tiếp (H). Tính tỉ số thể tích của (H') và (H)
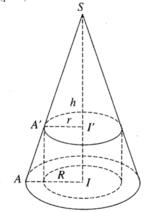
Giả sử đường cao SI của hình nón (H) cắt hai đáy của hình trụ (H') tại I và I'.
Khi đó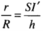 
Do đó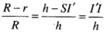 
Từ đó suy ra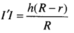 
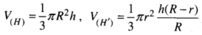
Do đó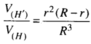 
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I đều thuộc (S) được gọi là hình nón nội tiếp mặt cầu (C). Gọi h là chiều cao của hình nón. Tìm h để thể tích của khối nón là lớn nhất.
A. 4 r 3
B. r 3
C. r 6
D. 7 r 6
Đáp án A.
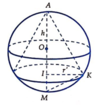
Kí hiệu như hình vẽ.
Ta thấy I K = r ' là bán kính đáy của hình chóp, A I = h là chiều cao của hình chóp.
Tam giác vuông tại K có IK là đường cao
⇒ I K 2 = A I . I M ⇒ r ' 2 = h . 2 r − h
Ta có V c o h p = 1 3 . π r ' 2 . h = 1 3 . π . h . h . 2 r − h = 4 3 π . h 2 . h 2 2 r − h .
Áp dụng bất đẳng thức Cauchy ta có
h 2 . h 2 . 2 r − h ≤ h 2 + h 2 + 2 r − h 3 27 = 8 r 3 27
⇔ V c h o p ≤ 4 3 π . 8 r 3 27 = 32 81 . π r 3
Dấu bằng xảy ra khi h 2 = 2 r − h ⇔ h = 4 r 3 . Vậy ta chọn A
