Cho hàm số y = f x có bảng biến thiên như sau:
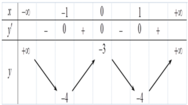
Hàm số đạt cực đại tại điểm x 0 bằng
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) có bảng biến thiên như sau:
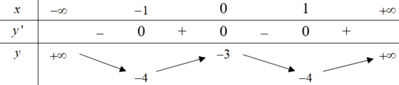
Hàm số đạt cực đại tại điểm x 0 bằng:
A. 0
B. -4
C. 1
D. -3
Cho hàm số y=f(x) có bảng biến thiên như sau
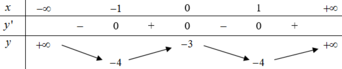
Hàm số đạt cực đại tại điểm x 0 bằng
A. 0
B. -4
C. 1
D. -3
Cho hàm số y=f(x) có bảng biến thiên như sau
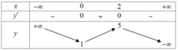
Hàm số đạt cực đại tại điểm
A. x=0
B. x=2
C. x=5
D. x=1
Đáp án B
Từ BBT ta thấy hàm số đạt cực đại tại x=2
Cho hàm số y=f(x) có bảng biến thiên như sau
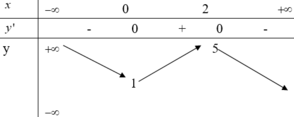
Hàm số đạt cực đại tại điểm
A. x=1
B. x=0
C. x=5
D. x=2
Cho hàm số y = f ( x ) có bảng biến thiên như sau
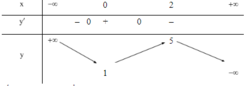
Hàm số đạt cực đại tại điểm
A. x = 1
B. x = 0
C. x = 5
D. x = 2
Hàm số đạt cực đại tại x = 2 và đạt giá trị cực đại tại y = 2
Đáp án cần chọn là D
Cho hàm số y = f ( x ) xác định trên R, có bảng biến thiên như sau. Hàm số y = f ( x ) đạt cực đại tại điểm
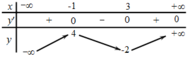
A. x=4
B. x=-2
C. x=-1
D. x=3
Cho hàm số y=f(x) có bảng biến thiên như sau
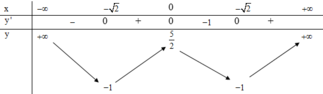
Hàm số y=f(x) đạt cực đại tại
A. x = - 2
B. x = - 1
C. x = 2
D. x = 0
Đáp án D
Phương pháp:
Quan sát bảng biến thiên, tìm điểm mà f’(x)=0 hoặc f’(x) không xác định.
Đánh giá giá trị của f’(x) và chỉ ra cực đại, cực tiểu của hàm số y = f(x):
- Cực tiểu là điểm mà tại đó f’(x) đổi dấu từ âm sang dương.
- Cực đại là điểm mà tại đó f’(x) đổi dấu từ dương sang âm.
Cách giải:
Quan sát bảng biến thiên, ta thấy: Hàm số y = f(x) đạt cực đại tại x = 0
Cho hàm số y=f(x) có bảng biến thiên như sau
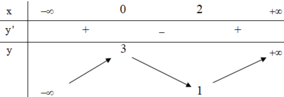
Hàm số đã cho đạt cực đại tại
A. 2
B. 1
C. 0
D. 3
Cho hàm số y = f(x) xác định trên R, có bảng biến thiên sau
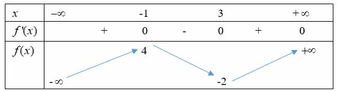
Hàm số y = f(x) đạt cực đại tại điểm
A. x = 4
B. x = -2
C. x = -1
D. x = 3
Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như sau:
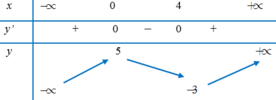
Hàm số đạt cực đại tại điểm nào trong các điểm dưới đây?
A. x = -3
B. x = 5
C. x = 4
D. x = 0
Đáp án D.
Từ bảng biến thiên của hàm số ta có hàm số đạt cực đại tại x = 0 , y C D = 5 ; hàm số đạt cực tiểu tại x = 4 , y C T = − 3. Do đó phương án đúng là D.
Phân tích phương án nhiễu.
Phương án A: Sai do HS nhầm với giá trị cực tiểu của hàm số.
Phương án B: Sai do HS nhầm với giá trị cực đại của hàm số.
Phương án C: Sai do HS nhầm với điểm cực tiểu của hàm số.