Trong Oxyz xét các mặt cầu bán kính bằng 1 và đều tiếp xúc với cả 3 mặt phẳng tọa độ. Gọi (S) là mặt cầu tiếp xúc trong với tất cả các mặt cầu trên. Tính bán kính R của (S).

Xét tám mặt cầu có bán kính bằng 1 và các mặt cầu này đều tiếp xúc với cả ba mặt phẳng tọa độ. Tìm bán kính mặt cầu (S) mà cả tám mặt cầu kể trên đều tiếp xúc trong với (S)

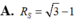
Mặt cầu đi qua A(4; -5; 5) và tiếp xúc các mặt phẳng tọa độ có bán kính lớn nhất (R_max) là:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) đi qua điểm M(2;5;-2) và tiếp xúc với mặt phẳng α : x = 1 , β : y = 1 , γ : z = - 1 .  Bán kính của mặt cầu (S) bằng:

A. 4   

B. 1

C.  3 2

D. 3

Trong không gian với hệ tọa độ Oxyz, xét các điểm A 0 ; 0 ; 1 ,   B m ; 0 ; 0 ,   C 0 ; n ; 0 ,  D 1 ; 1 ; 1 với m > 0, n > 0 và m + n = 1 . Biết rằng khi m, n thay đổi, tồn tại một mặt cầu cố định tiếp xúc với mặt phẳng (ABC) và đi qua D. Tính bán kính R của mặt cầu đó.

A. R = 1

B.  R = 2 2

C. R = 3 2

D. R = 3 2

Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng α :   x = 1 , β :   y = - 1 , γ : z = 1 . Bán kính mặt cầu (S) bằng:

A. 3

B. 1

C.  3 2

D.  33

Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng α :   x = 1 , β :   y = - 1 , γ :   z = 1 . Bán kính mặt cầu (S) bằng:

A. 3

B. 1

C.  3 2

D.  33

Trong không gian với hệ tọa độ Oxyz, cho A(2;11;-5) và mặt phẳng P : 2 m x + m 2 + 1 y + m 2 − 1 z − 10 = 0 . Biết rằng khi m thay đổi, tồn tại hai mặt cầu cố định tiếp xúc với (P) và cùng đi qua A. Tìm tổng bán kính của hai mặt cầu đó

A.  2 2

B.  5 2

C.  7 2

D.  12 2  

Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P : x − y + z = 0  và mặt cầu (S) có tâm I 1 ; − 1 ; 1  và bán kính R = 3. Từ một điểm M thuộc mặt phẳng (P) kẻ một đường thẳng tiếp xúc với mặt cầu S tại điểm N. Tính khoảng cách từ M tới gốc tọa độ biết rằng MN = 4.

A. 19

B.  2 2

C.  22

D. 5