Cho hàm số y = f(x) là hàm số chẵn và liên tục trên đoạn - π ; π thỏa mãn ∫ 0 π f x d x = 2018 . Tích phân ∫ - π π f x 2018 x + 1 d x bằng
A. 2018
B. 4036
C. 0
D. 1 2018
Cho hàm số y = f(x) là hàm số chẵn, liên tục trên đoạn [-1;1] và thỏa mãn ∫ 0 1 2 f x d x = 3 , ∫ 1 4 1 2 f 2 x d x = 10 . Tính I = ∫ - π 2 0 cos x f sin x d x
A. I = 7
B. I = 23
C. I = 13
D. I = 8
Chọn B.
Phương pháp : Sử dụng phương pháp đổi biến.
Cách giải : Ta có :


Cho hàm số y = f(x) là hàm số chẵn, liên tục trên đoạn [-1;1] và thỏa mãn ∫ 0 1 2 f ( x ) d x = 3 ; ∫ 1 4 1 2 f ( 2 x ) d x = 10 . Tính ∫ - π 2 0 cos f ( sin x ) d x
A. I = 7
B. I = 23
C. I = 13
D. I = 8
Cho hàm số y=f(x) là hàm số chẵn, liên tục trên đoạn [-1;1] và thỏa mãn ∫ 0 1 2 f ( x ) d x = 3 , ∫ 1 4 1 2 f ( 2 x ) d x = 1 . Tính I= ∫ - π 2 0 cos x f ( sin x ) d x
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Cho hàm số y = f(x) liên tục trên R và là hàm số chẵn, biết ∫ - 1 1 f ( x ) 1 + e x d x = 1 . Tính ∫ - 1 1 f ( x ) d x
A. 1
B. 2
C. 4
D. 1/2
Đáp án B
Phương pháp: Đặt t = - x
Cách giải: I = ∫ - 1 1 f ( x ) 1 + e x d x = 1 (1)
Đặt t = - x => dt = - dx
Đổi cận 
Khi đó:
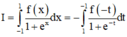
 (do là hàm chẵn)
(do là hàm chẵn)
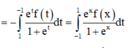
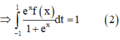
Từ (1), (2), suy ra
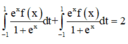
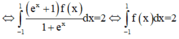
Cho hàm số y = f(x) liên tục trên R và là hàm số chẵn, biết ∫ - 1 1 f ( x ) 1 - e x d x = 1 tính ∫ - 1 1 f ( x ) d x
A. 1
B. 2
C. 4
D. 1/2
Cho hàm số y = f(x) là hàm số chẵn, liên tục trên - 1 ; 1 và ∫ - 1 1 f x d x = 6 . Kết quả của ∫ - 1 1 f x 1 + 2018 x d x bằng
A. 2
B. 3
C. 4
D. 5
Cho y = f(x) là hàm số chẵn, liên tục trên biết đồ thị hàm số y = f(x) đi qua điểm
M - 1 2 ; 4 và ∫ 0 1 2 f t d t = 3 , tính I = ∫ - π 6 0 sin 2 x f ' sin x d x
A. I = 10
B. I = -2
C. I = 1
D. I = -1
Đáp án B
Vì f(x) là hàm chẵn
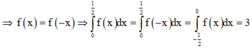
Đặt

Khi đó
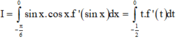
Đặt
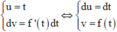
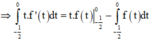
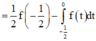 mà
mà 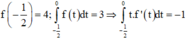 .
.
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f(2sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
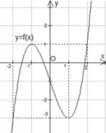
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]