Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Số nghiệm của phương trình 2 f x − 1 − 3 = 0 là:
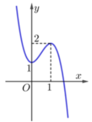
A. 1
B. 4
C. 3
D. 2
Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ bên
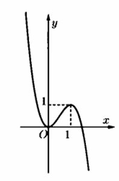
Tìm số nghiệm của phương trình f(x) = x
A. 0
B. 1
C. 2
D. 3
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình f(x)=3
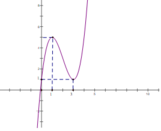
A. 0
B. 2
C. 1
D. 3
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Phương trình f(x) = -3 có số nghiệm là
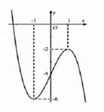
A. 0
B. 1
C. 2
D. 3
Cho hàm số f(x) có đồ thị như hình vẽ bên
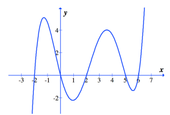
Số nghiệm của phương trình f(x)-2=0 là
A. 5.
B. 3.
C. 1.
D. 6.
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Hàm số y= f'(x) có đồ thị như hình vẽ bên dưới:
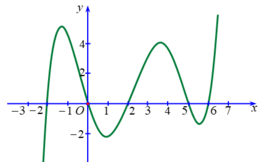
Số nghiệm thuộc đoạn [-2;6] của phương trình f(x) = f(0) là
A. 5
B. 2
C. 3
D. 4
Cho hàm số f ( x ) = m x 4 + n x 3 + p x 2 + q x + r . Hàm số y = f'(x) có đồ thị như hình vẽ bên. Tập nghiệm của phương trình f(x) = r có số phần tử là
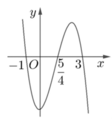
A.4.
B. 3.
C. 1.
D. 2.
Cho hàm số y = f(x) có đạo hàm liên tục trên R, đồ thị của hàm số y = f′(x) như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(x) = f(0) trên đoạn [−3;6] là
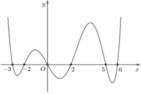
A. 4
B. 3.
C. 5.
D. 2.
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(f(x))=f(x) bằng
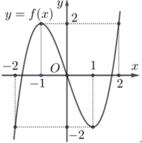
A. 7
B. 3
C. 6
D. 9
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(f(x)) =0 bằng

A. 7
B. 3
C. 5
D. 9
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(f(x))=0 bằng
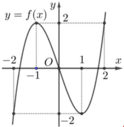
A. 7
B. 3
C. 5
D. 9

Vậy phương trình đã cho có tất cả 9 nghiệm.
Chọn đáp án D.