Tất cả các đường tiệm cận của đồ thị hàm số y = x − x 2 − 4 x 2 − 4 x + 3 là
A. y = 1 và x = 3
B. y = 0, y = 1 và x = 3
C. y = 0, x = 1 và x = 3
D. y = 0 và x = 3
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hàm số
y
=
f
(
x
)
=
a
x
4
+
b
x
2
+
c
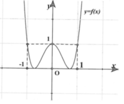
có đồ thị như hình bên dưới. Tìm tổng tất cả các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
=
x
(
x
-
1
)
f
(
x
)
-
1
![]()
![]()
![]()
![]()
Tất cả các đường tiệm cận đứng của đồ thị hàm số y = x - 1 x 2 - x là
A. x=1.
B. x=0;x=1.
C. x=0.
D. x=0;x=-1.
Tìm tất cả các đường tiệm cận của đồ thị hàm số y = x + 3 x 2 + 1
A. y = ±1.
B. x = 1.
C. y = 1.
D. y = -1.
Chọn A
Vì TXĐ của hàm số là R nên đồ thị hàm số không có tiệm cận đứng.
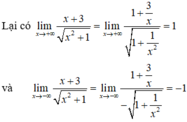
Vậy đồ thị hàm số có hai đường tiệm cận ngang là y = ±1
Tìm tất cả các đường tiệm cận của đồ thị hàm số y = x - x 2 - 4 x 2 - 4 x + 3 là
A. y = 1 và x = 3
B. y = 0, y = 1 và x = 3
C. y = 0 và x = 3, x = 1
D. y = 0 và x = 3
Cho hàm số y = x 2 + x + 1 - x 2 - x x - 1 . Tất cả các đường thẳng là đường tiệm cận của đồ thị hàm số trên là
A. x = 1 ; y = 0 ; y = 2 ; y = 1
B. x = 1 ; y = 2 ; y = 1
C. x = 1 ; y = 0 ; y = 1
D. x = 1 ; y = 0
Cho hàm số y = x 2 + x + 1 - x 2 - x x - 1 Tất cả các đường thẳng là đường tiệm cận của đồ thị hàm số trên là
A. x = 0; y = 0; y = 2; y = 1
B. x = 1; y = 2; y = 1
C. x = 1; y = 0; y = 1
D. x = 1; y = 0
Chọn D.
Ta có tập xác định của hàm số ![]()
Ta có:
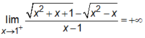
nên x = 1 là đường TCĐ của đồ thị hàm số.
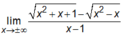
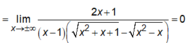
nên đường thẳng y = 0 là TCN của đồ thị hàm số
Đồ thị của hàm số y = f ( x ) = cos x + 1 ( x - 1 ) ( x - 2 ) có tổng tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A. 0
B. 3
C. 2
D. 1
Cho hàm số y = x - 2 m x 2 - 2 x + 4 . Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)?
A. 1.
B. 3.
C. 0.
D. 2.
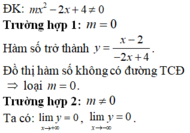
Suy ra đồ thị hàm số có 1 đường TCN y = 0.
Do đó đồ thị hàm số có đúng 2 đường tiệm cận đồ thị hàm số có đứng 1 đường tiệm cận đứng phương trình m x 2 - 2 x + 4 = 0 có nghiệm kép hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm x = 2.
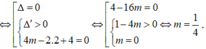
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn A
Cho hàm số y = x − 1 m x 2 − 2 x + 3 . Tìm tất cả các giá trị của m để đồ thị hàm số có ba đường tiệm cận
A. m ≠ 0 m ≠ − 1 m < 1 5
B. m ≠ 0 m ≠ − 1 m < 1 3
C. m ≠ 0 m < 1 3
D. m < 1 5 m ≠ 0
Đáp án B
Đồ thị hàm số có 3 tiệm cận thì phương trình m x 2 − 2 x + 3 = 0 phải có hai nghiệm phân biệt khác 1.