Khi a = 1, ta có phương trình:

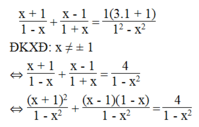
⇔ x + 1 2  + (x – 1)(1 – x) = 4

⇔ x 2  + 2x + 1 + x –  x 2  – 1 + x = 4

⇔ 4x = 4 ⇔ x = 1 (loại)

Vậy phương trình vô nghiệm.

Khi a = 0, ta có phương trình:

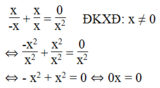
Phương trình nghiệm đúng với mọi giá trị của x ≠ 0

Vậy phương trình có nghiệm x ∈ R / x  ≠  0.

Thay x = 1/2 vào phương trình, ta có:

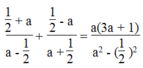
ĐKXĐ: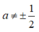 

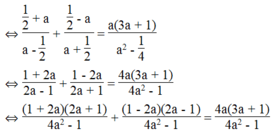
⇔ (1 + 2a)(2a + 1) + (1 – 2a)(2a – 1) = 4a(3a + 1)

⇔ 2a + 1 + 4 a 2  + 2a + 2a – 1 – 4 a 2  + 2a = 12 a 2  + 4a

⇔ 12 a 2  – 4a = 0 ⇔ 4a(3a – 1) = 0 ⇔ 4a = 0 hoặc 3a – 1 = 0

⇔ a = 0 (thỏa mãn) hoặc a = 1/3 (thỏa mãn)

Vậy khi a = 0 hoặc a = 1/3 thì phương trình  x + a a - x + x - a a + x = a 3 a + 1 a 2 - x 2  có nghiệm x = 1/2

1. a = 3 thì phương trình trở thành:

\(\frac{x+3}{3-x}-\frac{x-3}{3+x}=\frac{-3\left[3.\left(-3\right)+1\right]}{\left(-3\right)^2}-x^2\)

\(\Leftrightarrow\frac{\left(x+3\right)^2+\left(3-x\right)^2}{\left(3-x\right)\left(3+x\right)}=\frac{-3\left[-9+1\right]}{9}-x^2\)

\(\Leftrightarrow\frac{x^2+6x+9+x^2-6x+9}{\left(3-x\right)\left(3+x\right)}=\frac{-3.\left(-8\right)}{9}-x^2\)

\(\Leftrightarrow\frac{2x^2+18}{9-x^2}=\frac{24}{9}-x^2\)

\(\Leftrightarrow\frac{2x^2+18}{9-x^2}+x^2=\frac{24}{9}\)

\(\Leftrightarrow\frac{2x^2+18+9x^2-x^4}{9-x^2}=\frac{24}{9}\)

\(\Leftrightarrow\frac{11x^2+18-x^4}{9-x^2}=\frac{24}{9}\)

\(\Leftrightarrow99x^2+18-9x^4=216-24x^2\)

\(\Leftrightarrow9x^4-123x^2+198=0\)

Đặt \(x^2=t\left(t\ge0\right)\)

Phương trình trở thành \(9t^2-123t+198=0\)

Ta có \(\Delta=123^2-4.9.198=8001,\sqrt{\Delta}=3\sqrt{889}\)

\(\Rightarrow\orbr{\begin{cases}t=\frac{123+3\sqrt{889}}{18}=\frac{41+\sqrt{889}}{6}\\t=\frac{123-3\sqrt{889}}{18}=\frac{41-\sqrt{889}}{6}\end{cases}}\)

Lúc đó \(\orbr{\begin{cases}x^2=\frac{41+\sqrt{889}}{6}\\x^2=\frac{41-\sqrt{889}}{6}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\pm\sqrt{\frac{41+\sqrt{889}}{6}}\\x=\pm\sqrt{\frac{41-\sqrt{889}}{6}}\end{cases}}\)

Vậy pt có 4 nghiệm \(S=\left\{\pm\sqrt{\frac{41+\sqrt{889}}{6}};\pm\sqrt{\frac{41-\sqrt{889}}{6}}\right\}\)

Sửa)):

a = -3 mà ghi lôn a = 3.giải tương tự như 3

\(\Delta=\left(m+1\right)^2-4\left(2m-2\right)=m^2-6m+9=\left(m-3\right)^2\ge0\) ; \(\forall m\)

\(\Rightarrow\) Phương trình luôn có nghiệm với mọi m

Đk:\(a\ne\pm x\)

Pt \(\Leftrightarrow\dfrac{\left(a+x\right)^2-\left(x-a\right)\left(a-x\right)}{\left(a-x\right)\left(a+x\right)}=\dfrac{a\left(3a+1\right)}{a^2-x^2}\)

\(\Leftrightarrow\dfrac{2\left(a^2+x^2\right)}{a^2-x^2}=\dfrac{a\left(3a+1\right)}{a^2-x^2}\)

\(\Leftrightarrow2a^2+2x^2=3a^2+a\)

\(\Leftrightarrow a^2+a-2x^2=0\) (1)

Thay \(x=\dfrac{1}{2}\) vào (1) ta được:

\(a^2+a-2\left(\dfrac{1}{2}\right)^2=0\)

\(\Leftrightarrow a^2+a-\dfrac{1}{2}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=\dfrac{-1+\sqrt{3}}{2}\\a=\dfrac{-1-\sqrt{3}}{2}\end{matrix}\right.\) (tm)

Vậy...