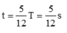Một con lắc lò xo nằm ngang dao động theo phương trình x = 5cos(2πt – π/3) (x tính bằng cm; t tính bằng s). Kể từ t = 0, lò xo không biến dạng lần đầu tại thời điểm
A. 5/12 s
B. 1/6 s
C. 2/3 s
D. 11/12 s
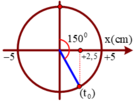
Một con lắc lò xo nằm ngang dao động theo phương trình x=5cos(2πt-π/3)(cm) ( x tính bằng cm; t tính bằng s). Kể từ t=0, lực đàn hồi đổi chiều lần đầu tại thời điểm
A. 2/3 s.
B. 11/12 s.
C. 1/6 s.
D. 5/12s
Đáp án D
Phương pháp: Sử dụng lí thuyết về lực đàn hồi trong dao động điều hòa của CLLX ngang và đường tròn lượng giác
Cách giải:
+ Đối với CLLX ngang thì lực đàn hồi đổi chiều tại VTCB
+ Biểu diễn trên đường tròn lượng giác :
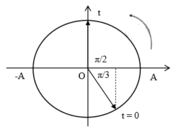
Góc quét được:
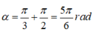
=> Từ t = 0 thì vật đi qua VTCB lần đầu tại thời điểm:
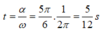
Một con lắc lò xo nằm ngang dao động điều hòa với phương trình x=5cos(10πt+π/3)cm. Chiều dài tự nhiên của lò xo là 20cm. Tính lmax,lmin của lò xo trong quá trình vật dao động.
\(l_{max}=l_0+\Delta l+A\Rightarrow\left\{{}\begin{matrix}A=5cm=0,02m\\\Delta l=\dfrac{g}{\omega^2}=\dfrac{10}{\left(10\right)^2}=0,1m\\l_0=0,2m\end{matrix}\right.\)
=> \(l_{max}=0,2+0,1+0,02=0,32\left(m\right)=32cm\)
\(l_{min}=l_0+\Delta l-A=0,2+0,1-0,02=0,28\left(m\right)=28\left(cm\right)\)
Vậy ...
Một con lắc lò xo nằm ngang dao động điều hòa với phương trình x = 5cos (10πt + π/3)cm. Chiều dài tự nhiên của lò xo là 20 cm Tính lực đàn hồi cực đại và cực tiểu của lò xo biết khối lượng vật nặng là 100 g lấy π²= 10
Con lắc lò xo nằm ngang dao động điều hoà với phương trình x=5cos(πft+ π/2) cm. Lò xo có độ cứng k = 50 N/m. Chọn mốc thế năng ở vị trí cân bằng. Phát biểu nào sau đây là sai?
A. Động năng con lắc lò xo biến thiên tuần hoàn với tần số f.
B. Cơ năng của con lắc lò xo là 0,0625 J.
C. Thế năng con lắc lò xo biến thiên tuần hoàn với tần số 2f.
D. Trong một chu kì dao động có hai lần động năng đạt giá trị cực đại.
Cho một con lắc lò xo dao động điều hoà với phương trình x = 5cos(20t + π/6) (cm). Biết vật nặng có khối lượng m = 200g. Cơ năng của con lắc trong quá trình dao động bằng:
A. 0,1mJ.
B. 0,01J.
C. 0,1J.
D. 0,2J.
Chọn C
W= 1 2 m . w 2 A 2 = 1 2 0 , 2 . 20 2 . ( 5 . 10 - 2 ) 2 = 0 , 1 J
Một con lắc lò xo nằm ngang dao động theo phương trình
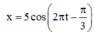
(x tính bằng cm; t tính bằng s). Kể từ , lò xo không biến dạng lần đầu tại thời điểm
A. 5/12 s
B.1/6 s
C.2/3 s
11/12 s
Đáp án A
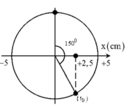
Lò xo nằm ngang không biến dạng khi vật đi qua vtcb (x = 0).
Góc quay từ t = 0 đến x = 0 lần đầu tiên
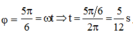
Bài 2: Một con lắc lò xo nằm ngang dao động điều hòadọc theo trục tọa độ Ox, gốc O ở vị trí cân bằng, chiều dương hướng ra xa đầu cố định của lò xo, với phương trình: x = 6cos(10πt + π/3) cm. Chiều dài tự nhiên của lò xo là 20 cm. Chiều dài của con lắc ở vị trí cân bằng . (mình đag cần rất gấp ạ!!)
Vì con lắc lò xo nằm ngang nên `\Delta l_0=0`
`=>l_0 =l_[CB]=20(cm)`.
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5 cos 2 π t − π 3 (x tính bằng cm; t tính bằng s). Kể từ t = 0 , lò xo không biến dạng lần đầu tại thời điểm
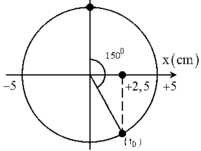
A. 5 12 s
B. 1 6 s
C. 2 3 s
D. 11 12 s
Đáp án A
Lò xo nằm ngang không biến dạng khi vật đi qua vtcb (x = 0)
Góc quay từ t = 0 đến x = 0 lần đầu tiên: φ = 5 π 6 = ω t ⇒ t = 5 π / 6 2 π = 5 12 s
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5 cos 2 π t - π 3 (x tính bằng cm; t tính bằng s). Kể từ t = 0, lò xo không biến dạng lần đầu tại thời điểm
A. 5 12 s
B. 1 6 s
C. 2 3 s
D. 11 12 s
Chọn đáp án A
Lò xo không biến dạng tại vị trí cân bằng.
→ Biểu diễn dao động của vật tương ứng trên đường tròn.
Từ hình vẽ ta thấy rằng khoảng thời gian tương ứng là