Hình vẽ bên là đồ thị C của hàm số y = f x .
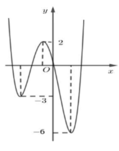
Giả sử m là tham số thực nhận giá trị thuộc nửa khoảng ( 0 ; 3 ] . Hỏi hàm số y = f x - 1 + m có thể có bao nhiêu điểm cực trị
A. 5 hoặc 7 điểm
B. 3 điểm
C. 6 hoặc 8 điểm
D. 4 điểm
Hình vẽ bên là đồ thị (C) của hàm số y = f(x).
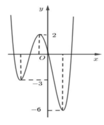
Giả sử m là tham số thực nhận giá trị thuộc nửa khoảng (0;3]. Hỏi hàm số y = f x - 1 + m có thể có bao nhiêu điểm cực trị
A. 5 hoặc 7 điểm
B. 3 điểm
C. 6 hoặc 8 điểm
D. 4 điểm
Chọn A.
Phương pháp : Sử dụng các phép suy đồ thị.

Lấy đối xứng phần bên dưới trục hoành qua trục hoành và bỏ phần bên dưới trục hoành.
Do đó:

Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(2sinx+1)=m có nghiệm thuộc nửa khoảng [ 0 ; π 6 ) là

A. (-2;0]
B. (0;2]
C. [-2;2]
D. (-2;0)
Đặt t=2sinx+1 với
![]()
![]()
![]()
Phương trình trở thành: f(t)=m có nghiệm ![]()
Chọn đáp án A.
Cho hàm số y=f(x) là hàm đa thức hệ số thực. Hình vẽ bên là đồ thị của hai hàm số y=f(x) và y=f'(x) . Phương trình f(x)= m e x có hai nghiệm thực phân biệt thuộc đoạn [0;2] khi và chỉ khi m thuộc nửa khoảng [a;b). Giá trị của a+b gần nhất với giá trị nào dưới đây ?
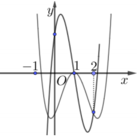
A. 0,27.
B. −0,54.
C. −0,27.
D. 0,54.
Cho hàm số y=f(x) là hàm đa thức với hệ số thực. Hình vẽ bên dưới là một phần đồ thị của hai hàm số: y=f(x) và y=f'(x)
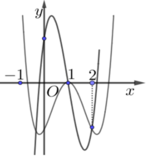
Tập các giá trị của tham số m để phương trình f ( x ) = m e x có hai nghiệm phân biệt trên [0;2] là nửa khoảng [a;b). Tổng a+b gần nhất với giá trị nào sau đây?
A. -0.81
B. -0.54
C. -0.27
D. 0.27
Cho hàm số y = f (x) liên tục trên ℝ và có đồ thị như hình vẽ bên.
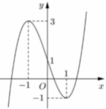
Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) = m có nghiệm thuộc khoảng (0; π ) là
A. [-1;3)
B. (-1;1)
C. (-1;3)
D. [-1;1 )
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sinx)=m có nghiệm thuộc khoảng 0 ; π là
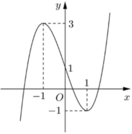
A. (-1;3)
B. (-1;1)
C. (-1;3)
D. (-1;1)
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(2sin x +1) = m có nghiệm thuộc nửa khoảng [ 0 ; π 6 ) là:
A. (-2;0]
B. (0;2]
C. [-2;2)
D. (-2;0)
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(f(sinx))=m có nghiệm thuộc khoảng 0 ; π là
A. [-1;3)
B. (-1;1)
C. (-1;3]
D. [-1;1)
Cho hàm số y = f ( x ) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f sin x = m có nghiệm thuộc khoảng là
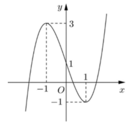
A. (-1;3)
B. (-1;1)
C. (-1;3)
D. (-1;1)
Chọn đáp án D.
![]()
Do đó để phương trình f sin x = m có nghiệm trong khoảng (0;p)
thì phương trình f t = m có nghiệm t ∈ ( 0 ; 1 ]