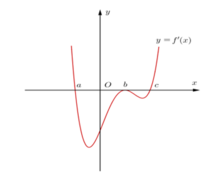
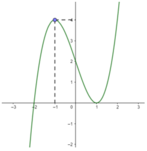
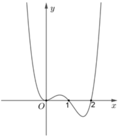
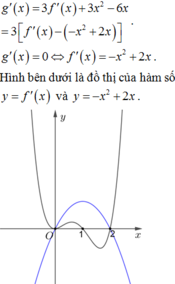
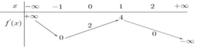
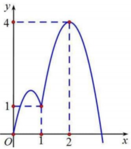
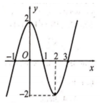
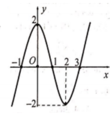
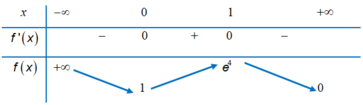
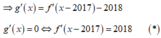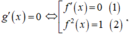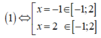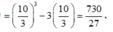Cho hàm số y = f x liên tục trên tập số thực ℝ và hàm số g x = f x - 1 2 x 2 + x + 1 . Biết đồ thị của hàm số y = f ' x như hình vẽ dưới đây
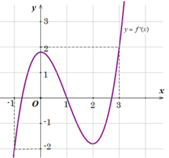
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số y = g x có 2 điểm cực tiểu và 1 điểm cực đại.
B. Đồ thị hàm số y = g x có 2 điểm cực tiểu và không có điểm cực đại.
C. Đồ thị hàm số y = g x có 1 điểm cực tiểu và 2 điểm cực đại.
D. Đồ thị hàm số y = g x có 3 điểm cực tiểu và 1 điểm cực đại.