Cho các hàm số y = f(x), y = g(x), y = f ( x ) + 3 g ( x ) + 1 . Hệ số góc tiếp tuyến của các đồ thị hàm số đã cho tại điểm có hoành độ x = 1 bằng nhau và khác 0. Khẳng định nào sau đây là đúng?
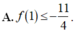
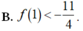
![]()
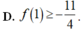
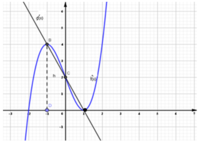
Cho hai hàm số y = f(x) và y = g(x) có đồ thị của hàm y = f '(x), y = g'(x) như hình vẽ. Tìm các khoảng đồng biến của hàm số y = f(x) - g(x)
A. - 1 ; 0 ; 1 ; + ∞
B. - ∞ ; - 1 ; 0 ; 1
C. 1 ; + ∞ ; - 2 ; - 1
D. - 2 ; + ∞
Cho hai hàm số y = f(x) và y = g(x) xác định trên R. Đặt S(x) = f(x) + g(x) và P(x) = f(x) g(x).
Xét các mệnh đề:
i) Nếu y = f(x) và y = g(x) là những hàm số chẵn thì y = S(x) và y = P(x) cũng là những hàm số chẵn
ii) Nếu y = f(x) và y = g(x) là những hàm số lẻ thì y = S(x) là hàm số lẻ và y = P(x) là hàm số chẵn
iii) Nếu y = f(x) là hàm số chẵn, y = g(x) là hàm số lẻ thì y = P(x) là hàm số lẻ
Số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. Tất cả đều sai
Cho hàm số y= f( x) có đạo hàm f ' ( x ) = x 2 ( x - 9 ) ( x - 4 ) 2 . Xét hàm số y= g( x) =f( x2) Trong các phát biểu sau; tìm số phát biểu đúng
I. Hàm số y = g( x) đồng biến trên( 3; +∞)
II. Hàm số y= g(x) nghịch biến trên( -∞; -3)
III. Hàm số y= g( x) có 5 điểm cực trị
IV. m i n x ∈ R g ( x ) = f ( 9 )
A. 1
B. 2
C. 3
D. 4
Ta có
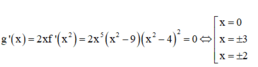
Bảng biến thiên của hàm số y= g( x)
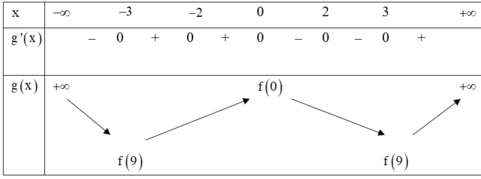
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞) hàm số nghịch biến trong khoảng (-∞; -3) .
Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3
Vậy có 3 khẳng định đúng là khẳng định I, II, IV
Chọn C.
Cho hàm số y= f( x) Đồ thị hàm số y= f’( x) như hình bên. Hỏi hàm số y= g(x) = f( x2) đồng biến trên khoảng nào trong các khoảng sau?
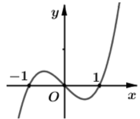
A. ( - ∞ ; - 1 )
B. (-1; + ∞ )
C. (-1; 0)
D. (0;1)
Cho hàm số y= f(x) . Đồ thị hàm số y= f’(x) như hình bên. Hỏi hàm số y= g(x) = f(1-x2) nghịch biến trên khoảng nào trong các khoảng sau?
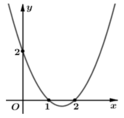
A. (1; 2)
B. (0; + ∞)
C. (-2; -1)
D. (-1; 1)
Cho hàm số y= f(x) . Đồ thị hàm số y= f’(x) như hình bên dưới
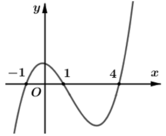
Hàm số g(x) = f( 3-x) đồng biến trên khoảng nào trong các khoảng sau?
A. ( - ∞ ; - 1 )
B. (-1; 2)
C. (2; 3)
D. (4; 7)
Cho hàm số y = f(x). Đồ thị hàm số y=f '(x) như hình bên dưới.
Hàm số g(x)=f(|3-x|) đồng biến trên khoảng nào trong các khoảng sau?
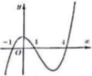
A. (4;7).
B. (2;3).
C. - ∞ ; - 1
D. (-1;2).
Cho hàm số y= f(x). Đồ thị hàm số y= f’(x) như hình dưới và f(-2) = f( 2) = 0
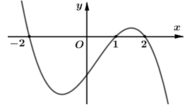
Hàm số g( x) = [ f( 3-x)]2 nghịch biến trên khoảng nào trong các khoảng sau?
A. (- 2; -1)
B. (1; 2)
C. (2; 5)
D. ( 5 ; + ∞ )
Cho hàm số y=f(x)=x; y=g(x)=-2x; y=h(x)=1; y=k(x)=5; y=z(x)=\(\frac{1}{x}\); y=t(x)=\(^{x^2}\). Trong các hàm số trên, hàm số nào có tính chất f(-x)=f(x)
Cho hàm số y=f(x) có đạo hàm f’(x) trên R. Hình vẽ bên là đồ thị của hàm số y=f’(x). Hàm số g ( x ) = f ( x - x 2 ) nghịch biến trên khoảng nào trong các khoảng dưới đây
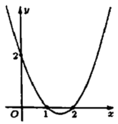
A. - ∞ ; 5 2
B. 3 2 ; + ∞
C. 1 2 ; + ∞
D. - ∞ ; 1 2