Cho hàm số f(x) và g(x) có đạo hàm trên đoạn [1;4] và thỏa mãn hệ thức: f ( 1 ) + g ( 1 ) = 4 g ( x ) = - x . f ' ( x ) ; f ( x ) = - x . g ' ( x ) . Tính tích phân ∫ 1 4 [ f ( x ) + g ( x ) ] dx
A. 8ln2.
B. 3ln2
C. 6ln2
D. 4ln2
Cho hàm số y = f(x) có đạo hàm f'(x). Hàm số y = f'(x) liên tục trên tập số thực và có bảng biến thiên như sau:
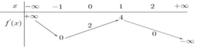
Biết rằng f(-1) = 10 3 , f(2) = 6. Giá trị nhỏ nhất của hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2] bằng
A. 10 3
B. 820 27
C. 730 27
D. 198
Chọn C
Xét hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2]
![]()
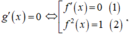
Từ bảng biến thiên, ta có:
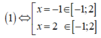
Và ![]() nên f(x) đồng biến trên [-1;2]
nên f(x) đồng biến trên [-1;2]
![]()
![]() nên (2) vô nghiệm
nên (2) vô nghiệm
Do đó, g'(x) = 0 chỉ có nghiệm là x = -1 và x = 2
Ta có ![]()
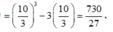
![]()
Vậy ![]()
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = x 2 ( x - 2 ) ( x 2 - 6 x + m ) , với mọi x ∈ R . Có bao nhiêu số nguyên m thuộc đoạn - 2019 ; 2019 để hàm số g ( x ) = f ( 1 - x ) nghịch biến trên khoảng - ∞ ; - 1
A. 2012
B. 2011
C. 2009
D. 2010
Cho hàm số y=f(x) liên tục trên R và có đạo hàm f ' x = x 2 x - 2 x 2 - 6 x + m với mọi x ∈ ℝ Có bao nhiêu số nguyên m thuộc đoạn [-2019;2019] để hàm số g(x)=f(1-x) nghịch biến trên khoảng - ∞ ; - 1
A. 2010
B. 2012
C. 2011
D. 2009
Cho hàm số y=f(x) có đạo hàm, liên tục trên đoạn [-3;3] và đồ thị hàm số y=f' (x) như hình vẽ bên. Biết f(1)=6 và g(x)=f(x)- ( x + 1 ) 2 2 .
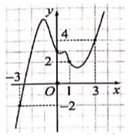
Kết luận nào sau đây là đúng
A. Phương trình g(x)=0 có đúng hai nghiệm thuộc [-3;3].
B. Phương trình g(x)=0 có đúng một nghiệm thuộc [-3;3].
C. Phương trình g(x)=0 không có nghiệm thuộc [-3;3].
D. Phương trình g(x)=0 có đúng ba nghiệm thuộc [-3;3].
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [-3;3] và đồ thị hàm số y=f'(x) như hình vẽ dưới đây
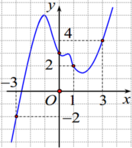
Biết f(1)=6 và g(x)=f(x) - x + 1 2 2 . Mệnh đề nào sau đây là đúng?
A. Phương trình g(x)=0 có đúng hai nghiệm thuộc [-3;3].
B. Phương trình g(x)=0 không có nghiệm thuộc [-3;3].
C. Phương trình g(x)=0 có đúng một nghiệm thuộc [-3;3].
D. Phương trình g(x)=0 có đúng ba nghiệm thuộc [-3;3].
Cho hàm số y=f(x)>0 xác định và có đạo hàm trên đoạn [0;1] và thỏa mãn các điều kiện sau: g(x)=1+2018 ∫ 0 x f ( t ) dt ; g ( x ) = f 2 ( x ) . Tính ∫ 0 1 ( g ( x ) dx ?
A. 1011/2.
B. 1009/2.
C. 2019/2.
D. 505
Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra 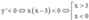 (vì g(1–x) < 0,
∀
x
∈
R
)
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f'(x) thoả mãn f'(x) = (1 - x)(x+2)g(x) + 2023 với g(x) < 0, ∀x∈R. Hàm số y = f(1-x) + 2023x + 2024 nghịch biến trên khoảng nào?
Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn [-3;3] và đồ thị y = f’(x) như hình vẽ. Đặt g x = 2 f x + x 2 + 4 . Biết f(1)=-24. Hỏi g(x) = 0 có bao nhiêu nghiệm thực?
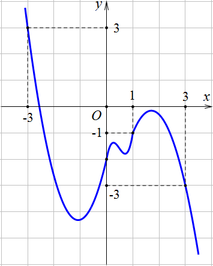
A. 1
B. 4
C. 2
D. 0