Môđun của số phức z=2-3i là
A.1
B.-1
C.2+3i
D. 13
Môđun của số phức z = 2 + 3 i - 1 + 5 i 3 - i là:
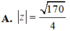
![]()
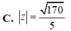
![]()
Môđun của số phức z = 2 + 3 i - 1 + 5 i 3 - i là:
A. z = 170 4
B. z = 170 3
C. z = 170 5
D. z = 170 8
Chọn C.
Phương pháp: Sử dụng định nghĩa mô đun của số phức.
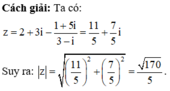
Cho số phức z = 2 - 3 i . Môđun của số phức w = 1 + i z
A. w = 26
B. w = 37
C. w = 5
D. w = 4
Cho số phức 2-3i. Môđun của số phức w=(1+i)z bằng
A. w = 26
B. w = 37
C. w = 5
D. w = 4
Cho số phức 2 – 3i. Môđun của số phức w = (1+i)z bằng
A. w = 26
B. w = 37
C. w = 5
D. w = 4
Cho số phức 2 - 3i Môđun của số phức w = (1 + i)z bằng
![]()
![]()
![]()
![]()
Số phức z thỏa mãn ( 2 + 3 i ) z + 1 - i z = 3 + 5 i Tìm môđun của số phức z.
A. 11
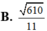
C. 9
![]()
Cho hai số phức z 1 = 1 + i và z 2 = 2 - 3 i . Môđun của số phức z = z 1 - z 2 bằng
A. 17
B. 15
C. 2 + 13
D. 13 - 2
Bài tập số 4: Tìm số phức liên hợp \(\overline{Z}\) và tính modun (|z|) của số phức sau.
a, z = 2 + 3i b, \(z=\left(2+3i\right)^3\)
c, \(z=\dfrac{2+3i}{1-2i}\) d, \(z=\sqrt{2}-\dfrac{4}{3}i\)