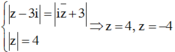Trong các số phức z thỏa mãn ( 12 - 5 i ) z + 17 + 7 i z - 2 - i = 13 . Tìm giá trị nhỏ nhất của z
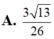
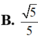
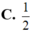
![]()
Trong các số phức z thỏa mãn | ( 12 - 5 i ) z + 17 + 7 i z - 2 - i | = 13 . Tìm giá trị nhỏ nhất của | z |
A . 3 13 26 .
B . 5 5 .
C . 1 2 .
D . 2 .
Trong các số phức z thỏa mãn 12 - 5 i z + 17 + 17 i z - 2 - i = 13 . Tìm giá trị nhỏ nhất của z .
A. 3 13 26
B. 5 5
C. 1 2
D. 2
Cho số phức z thỏa mãn 1 + i z + 5 ( 1 − i ) 1 + 2 i = 6 − 6 i . Trong các điểm dưới đây, điểm nào biểu diễn số phức z trong mặt phẳng phức Oxy?
A. M(2;5)
B. N(-2;5)
C. P(2;-5)
D. Q(-2;-5)
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
![]()
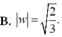
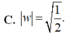
![]()
Xét các số phức z thỏa mãn điều kiện z - 3 + 2 i = 5 Trong mặt phẳng tọa độ Oxr, tập hợp các điểm biểu diễn các số phức w = z + 1 -i là
A. Đường tròn tâm I(4;-3), bán kính R = 5.
B. Đường tròn tâm I(-4;3), bán kính R = 5.
C. Đường tròn tâm I(-2;1), bán kính R = 5.
D. Đường tròn tâm I(3;-2), bán kính R = 5.
Cho số phức z thỏa mãn z - 1 2 - i + i = 5 . Biết rằng tập hợp biểu diễn số phức w = (1 - i)z + 2i có dạng x + 2 2 + y 2 = k . Tìm k.
A. k = 92
B. k = 100
C. k = 50
D. k = 96
Đáp án C.
Ta có z - 1 2 - i + i = 5 ⇔ z + 2 i = 5 ⇒ w + 2 = 1 - i z + 2 i = 5 2 . Vậy tập hợp điểm biểu diễn số phức w là đường tròn tâm I(-2;0) bán kính R = 5 2 , tức là đường tròn C : x + 2 2 + y 2 = 50 .
Cho số phức z thỏa mãn z - 1 2 - i + i = 5 . Biết rằng tập hợp biểu diễn số phức w = (1-i)z + 2i có dạng ( x + 2 ) 2 + y 2 = k Tìm k.
A. k = 92
B. k = 92
C. k = 50
D. k = 96
Đáp án C.
Ta có
z
-
1
2
-
i
+
i
=
5
![]()
![]()
Vậy tập hợp điểm biểu diễn số phức w là đường tròn tâm I(-2;0) bán kính R = 5 2 tức là đường tròn (C): ( x + 2 ) 2 + y 2 = 50
Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn 2 z - i = z - z ¯ + 2 i là:
A. Đường tròn tâm I(0;1), bán kính R=1
B. Đường tròn tâm I( 3 ;0), bán kính R= 3
C. Parabol y= x 2 4
D. Parabol x= y 2 4
Chọn C
Đặt ![]() và M(x;y) là điểm biểu diễn số phức z trên mặt phẳng phức
và M(x;y) là điểm biểu diễn số phức z trên mặt phẳng phức
Ta có
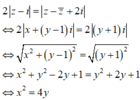
Trong các số phức z thỏa mãn |z - 3i| + | i z ¯ + 3| =10 , tìm số phức z có mô-đun nhỏ nhất.
A. z = 2 hoặc – 2
B. z= 3 hoặc – 3
C. z = 4 hoặc – 4
D. tất cả sai
Chọn C.
Áp dụng công thức: ![]()
Ta có: 

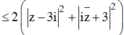
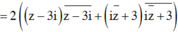
![]()
![]()
Giải bất phương trình 100 ≤ 4 ta có ![]() ta có 0 ≤ |z| ≤ 4
ta có 0 ≤ |z| ≤ 4
Vậy min|z| = 4 đạt được khi