Cho hàm số y = f x có đạo hàm cấp hai trên ℝ . Biết f ' 0 = 3 , f ' 2 = - 2018 và bảng xét dấu của như sau:

Hàm số y = f x + 2017 + 2018 x đạt giá trị nhỏ nhất tại điểm x 0 thuộc khoảng nào sau đây?
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) có đạo hàm cấp một f '(x) và đạo hàm cấp hai trên ℝ . Biết đồ thị của hàm số y = f x , y = f ' x v à y = f " x là một trong các đường cong C 1 , C 2 , C 3 ở hình vẽ bên. Hỏi đồ thị của hàm số y = f x , y = f ' x v à y = f " x lần lượt theo thứ tự nào dưới đây ?
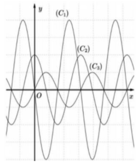
A. C 2 , C 1 , C 3
B. C 1 , C 2 , C 3
C. C 3 , C 2 , C 1
D. C 3 , C 1 , C 2
Đáp án là C
Các đồ thị hình vẽ bên chính là đồ thị của các hàm số lượng giác.
Cho hàm số y=f(x) có đạo hàm cấp hai liên tục trên ℝ . Biết f ' − 2 = − 8 , f ' 1 = 4 và đồ thị của hàm số f"(x) như hình vẽ dưới đây. Hàm số y = 2 f x − 3 + 16 x + 1 đạt giá trị lớn nhất tại x 0 thuộc khoảng nào sau đây?
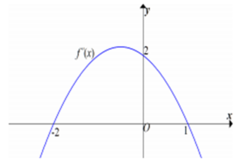
A. 0 ; 4
B. 4 ; + ∞
C. − ∞ ; 1
D. − 2 ; 1
B
Từ đồ thị của hàm số f"(x) ta có bảng biến
thiên của hàm số f'(x) như sau:
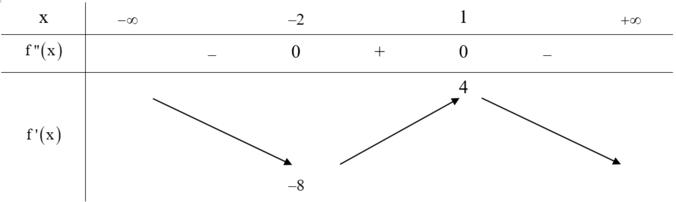

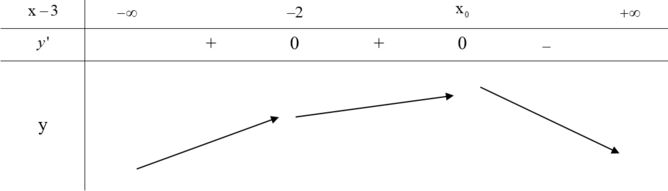
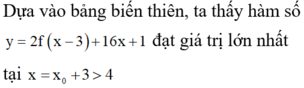
Xét các khẳng định sau
i) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực tiểu tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 > 0
ii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực đại tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 < 0
iii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và f ' ' x 0 = 0 thì hàm số không đạt cực trị tại x = x 0
Số khẳng định đúng trong các khẳng định trên là
A. 0
B. 1
C. 2
D. 3
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ thỏa mãn f'(x) -xf(x) = 0, f x > 0 , ∀ x ∈ ℝ và f(0) = 1. Giá trị của f(1) bằng?
A. 1 e .
B. 1 e .
C. e .
D. e.
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ thỏa mãn f ' x - x f x = 0 , f x > 0 , ∀ x ∈ ℝ và f(0) = 1. Giá trị của f(1) bằng?
A. 1 e
B. 1 e
C. e
D. e
Cho a , b ∈ ℝ , 0 < a < b, hàm số y = f(x) có đạo hàm trên ℝ thỏa mãn f'(x) < 0, ∀ x ∈ ( a ; b ) . Giá trị nhỏ nhất của hàm số đã cho trên đoạn [a;b] bằng
A. f(b)
B. f a + b 2
C. f(a)
D. f a b
Chọn A
Hàm số y = f(x) thỏa mãn f'(x) < 0 ∀ x ∈ ( a ; b ) nên hàm số nghịch biến trên (a;b).
Do đó ![]()
Cho hàm số f(x) có đạo hàm trên ℝ và f''(x) > 0, ∀ x ∈ ℝ . Biết f(1) = 2. Hỏi khẳng định nào sau đây có thể xảy ra?
A. f(2) + f(3) = 4
B. f(-1)= 2
C. f(2) = 1
D. f(2018) > f(2019)
Chọn B.
Xét đáp án A:
Ta có:
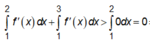
![]()
![]()
nên đáp án A không thể xảy ra.
Xét đáp án C:
Ta có:
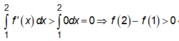
![]()
Nên phương án C không thể xảy ra.
Xét đáp án D:
Ta có:
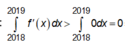
![]()
![]()
nên phương án D không thể xảy ra.
Bằng phương pháp loại suy, ta có đáp án B.
Tuy nhiên, ta có thể chỉ ra một hàm ![]() thỏa mãn đáp án B vì
thỏa mãn đáp án B vì

Cho hàm số f(x) có đạo hàm trên ℝ và f '(x) > 0, ∀ x ∈ ℝ . Biết f(1)=2. Hỏi khẳng định nào sau đây có thể xảy ra?
A. f(2) + f(3) = 4
B. f(-1) = 2
C. f(2) = 1
D. f(2018) > f(2019)
Cho hàm số y=f(x) có đạo hàm cấp hai trên R. Biết f '(0)=3,f '(2)=2018 và bẳng xét dấu của f ''(x) như sau:
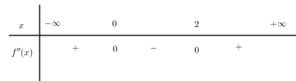
Hàm số y=f(x+2017)+2018x đạt giá trị nhỏ nhất tại điểm x0 thuộc khoảng nào sau đây?
A.![]()
B.![]()
C.![]()
D.![]()