Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Biết hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy. Hình chóp này có bao nhiêu mặt phẳng đối xứng
A. 4
B. 1
C. 0
D. 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = a , BC = 3 a . Hai mặt phẳng (SAB) và mặt phẳng (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC hợp với mặt đáy một góc 30 o . Tính thể khối chóp S.ABCD theo a.
A. 30 a 3 3 dvtt
B. 10 a 3 dvtt
C. 10 a 3 3 dvtt
D. 30 a 3 dvtt
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có A B = a , B C = 3 a . Hai mặt phẳng (SAB) và mặt phẳng (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC hợp với mặt đáy một góc 30 ° . Tính thể khối chóp S.ABCD theo a.
A. 30 a 3 d v t t
B. 10 a 3 d v t t
C. 10 3 a 3 d v t t
D. 30 a 3 3 d v t t
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = a, BC = 3a. Hai mặt phẳng (SAB) và mặt phẳng (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC hợp với mặt đáy một góc 30o. Tính thể khối chóp S.ABCD theo a.
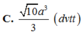
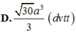
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 30 ° . Tính tỉ số 3 V a 3 biết V là thể tích của khối chóp S.ABCD?
A. 3 12
B. 3 12
C. 3 3
D. 8 3 3
Đáp án D
Vì S A ⊥ ( A B C D ) B C ⊥ A B ⇒ B C ⊥ ( S A B ) ⇒ S B C ; A B C D ^ = S B A ^
Tam giác SAB vuông tại A, có tan S B A ^ = S A A B ⇒ S A = 2 a . tan 30 ° = 2 a 3
Thể tích khối chóp S.ABCD là
V
=
1
3
S
A
.
S
A
B
C
D
=
1
3
2
a
3
4
a
2
=
8
a
3
2
9
Vậy tỉ số
3
V
a
3
=
24
a
3
3
9
:
a
3
=
8
3
3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 60 0 . Tính theo a thể tích khối chóp S.ABCD
A. 3 a 3
B. a 3 6 9
C. a 3 6 3
D. 3 2 a 3
Chọn đáp án C
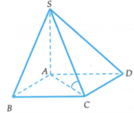
Ta có
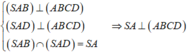
⇒ A C là hình chiếu của SC trên mặt phẳng (ABCD)
Lại có ABCD là hình vuông cạnh a nên A C = a 2
Tam giác SAC vuông tại A nên S A = A C . tan S C A ⏜ = a 6
Vậy thể tích khối chóp S.ABCD là V A B C D = a 3 6 3 (đvtt).
Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SBC) và (SAD) bằng 30 0 . Tính tỉ số 3 V a 3 biết V là thể tích của khối chóp S.ABCD.
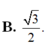
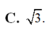
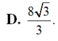
Cho hình chóp S.ABCD có đáy ABCD là một hình vuông cạnh a. Các mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC tạo với mặt phẳng đáy một góc 60 ° . Thể tích của khối chóp đã cho bằng:
A. a 3 6 5
B. a 3 6 3
C. a 3 6 4
D. a 3 6 9
Cho hình chóp S.ABCD có đáy ABCD là một hình vuông cạnh a. Các mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC tạo với mặt phẳng đáy một góc 60 0 . Thể tích của khối chóp đã cho bằng:
A . a 3 6 5
B . a 3 6 3
C . a 3 6 4
D . a 3 6 9
a