Gọi S là tập hợp tất cả các giá trị của m để đồ thị hàm số y = x 4 - 2 mx 2 + 2 m + m 4 có 3 điểm cực trị đồng thời các điểm cực trị của đồ thị lập thành tam giác có bán kính đường tròn ngoại tiếp bằng 1. Tính tổng các phần tử của S.
A.![]()
B.![]()
C. 0
D.![]()
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 2 + m x + m x - 1 có hai điểm cực trị A, B. Khi A B C ^ = 90 ∘ thì tổng bình phương tất cả các phần tử của S bằng
A. 1/16
B. 8
C. 1/8
D. 16
cho hàm số y=x2 - mx - m - 1 (m ϵ R) . Gọi S là tập hợp tất cả các giá trị của m để đồ thị đã cho cắt trục hoành tại 2 điểm phân biệt có hoành độ x1 ; x2 thỏa mãn |x1|+|x2|=4 . Tổng tất cả các phần tử của S là bao nhiêu
Cho hàm số y = x 3 - 3 x 2 + m x - m + 1 có đồ thị (C) và điểm A(0;2). Gọi S là tập hợp tất cả các giá trị nguyên của m để có ít nhất 2 tiếp tuyến của đồ thị (C) đi qua A . Tìm số phần tử của S.
![]()
![]()
![]()
![]()
Cho hàm số y = x - m x - 1 có đồ thị là và C m điểm A(-1;2). Gọi S là tập hợp tất cả các giá trị thực của m để có đúng một tiếp tuyến của đi qua A. Tổng tất cả các phần tử của S bằng.
A.1
B. 2
C. 3
D. 4
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để điểm cực tiểu của đồ thị hàm số y = x 3 + x 2 + m x - 1 nằm bên phải trục tung. Tìm số phần tử của tập hợp - 5 ; 6 ∩ S
A. 2
B. 5
C. 3
D. 4
Đáp án D
Xét hàm số y = x 3 + x 2 + m x - 1 có y ' = 3 x 2 + 2 x + m , ∀ x ∈ ℝ
Để hàm số có 2 điểm cực trị ⇔ y ' = 0 có 2 nghiệm phân biệt ⇔ 1 - 3 m > 0 ⇔ m < 1 3
Gọi x 1 , x 2 lần lượt là các điểm cực tiểu và cực đại của hàm số đã cho
Theo Viet, ta có x 1 + x 2 = - 2 3 x 1 x 2 = m 3 mà x 1 > 0 suy ra x 1 x 2 = m 3 < 0 ⇔ m < 0
Kết hợp m ∈ - 5 ; 6 mà m ∈ ℤ → m = - 4 ; - 3 ; - 2 ; - 1
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để điểm cực tiểu của đồ thị hàm số y = x 3 + x 2 + m x − 1 nằm bên phải trục tung. Tìm số phần tử của tập hợp − 5 ; 6 ∩ S
A. 2
B. 5
C. 3
D. 4
Gọi S là tập tất cả các giá trị của tham số m để đồ thị hàm số y = x 3 + 3 x 2 + 2 3 - 4 x 2 + 3 x + 2 + m x có tiệm cận ngang. Tổng các phần tử của S là
A. - 2
B. 2
C. - 3
D. 3
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để điểm cực tiểu của đồ thị hàm số y= x3+ x2+ mx-1 nằm bên phải trục tung. Tìm số phần tử nguyên của tập hợp - 5 ; 6 ∩ S
A. 2
B. 5
C. 3
D. 4
Ta có đạo hàm y’ = 3x2+ 2x+ m.
Hàm số có cực trị khi ∆ ' = 1 - 3 m > 0 ⇔ m < 1 3
Do hàm số có a=1>0 ⇒ x C T > x C D
Yêu cầu bài toán trở thành phương trình y’ = 0 có ít nhất 1 nghiệm dương
Do x 1 + x 2 = - 2 3 < 0 x 1 x 2 = m 3 ⇒ m < 0 là giá trị cần tìm.
Vậy - 5 ; 6 ∩ S = ( - 5 ; 0 )
Mà m nguyên nên chọn -4; -3; -2; -1. Có 4 giá trị thỏa mãn.
Chọn D.
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = - x - 1 3 + 3 m x - 1 - 2 có hai điểm cực trị cách đều gốc tọa độ. Tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là
A. 4.
B. 2 3
C. 1.
D. 5.

![]()
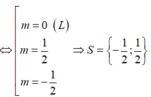
Vậy tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là 1.
Chọn C
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = - x - 1 3 + 3 m 2 x - 1 - 2 có hai điểm cực trị cách đều gốc tọa độ. Tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là
A. 4.
B. 2/3
C. 1.
D. 5.