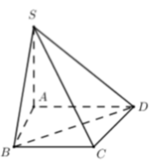
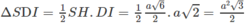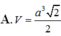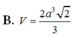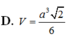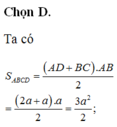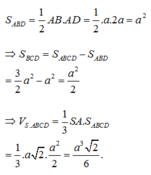Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D. SA vuông góc với mặt phẳng đáy (ABCD); AB = 2a, AC = CD=a. Mặt phẳng (P) đi qua CD và trọng tâm G của tam giác SAB cắt các cạnh SA, SB lần lượt tại M và N. Tính thể tích khối chóp S.CDMN theo thể tích khối chóp S.ABCD
A. V S . C D M N = 14 27 V S . A B C D
B. V S . C D M N = 4 27 V S . A B C D
C. V S . C D M N = 10 27 V S . A B C D
D. V S . C D M N = V S . A B C D 2









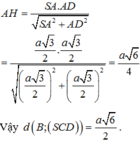
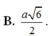
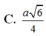
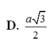
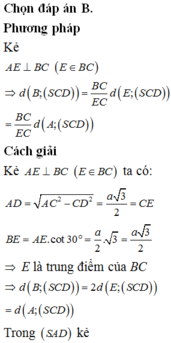

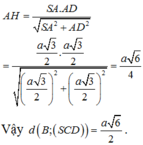
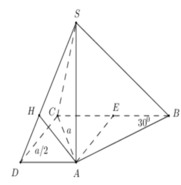
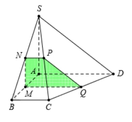


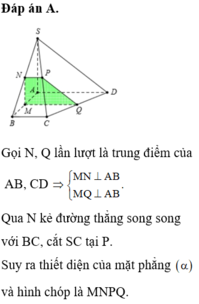


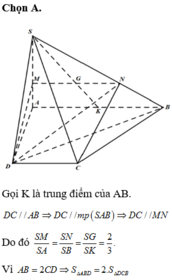
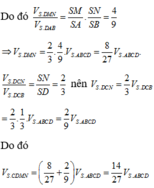
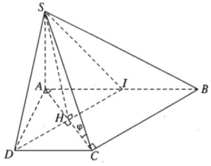
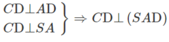
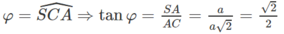
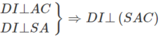
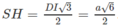 .
.