Nếu khối trụ có đường kính đường tròn đáy bằng a và chiều cao bằng 2a thì có thể tích bằng
![]()
![]()
![]()
![]()
Nếu một hình trụ có đường kính đường tròn đáy và chiều cao cùng bằng a thì có thể tích bằng
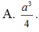
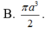
![]()
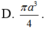
Một khối trụ có bán kính đường tròn đáy và chiều cao cùng bằng a thì có thể tích bằng
![]()
![]()
![]()
![]()
Khối trụ có đường kính đáy và chiều cao cùng bằng 2a có thể tích bằng
![]()
![]()
![]()
![]()
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB=2a. Thể tích khối tứ diện OO'AB theo a là
A. V = 3 a 3 8
B. V = 3 a 3 4 .
C. V = 3 a 3 6 .
D. V = 3 a 3 12 .
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt α là góc giữa AB và đáy. Tính tan α khi thể tích khối tứ diện OO’AB đạt giá trị lớn nhất.
A. tan α = 2
B. tan α = 1 2
C. tan α = 1 2
D. tan α = 1
Chọn B.
Cách 1:
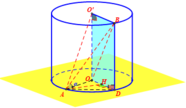

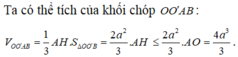
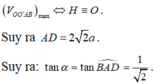
Cách 2:
Nhận xét: Nên thêm giả thiết AB chéo với OO’ để tứ diện OO’AB tồn tại.
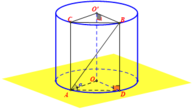

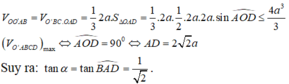
Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng a, chiều cao bằng a 2 . Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O’ lấy điểm O' sao cho AB' = 2a. Tính thể tích của khối tứ diện OO′B′A.
A. a 3 3 2
B. a 3 2 12
C. a 3 2 6
D. a 3 6
Thể tích của khối trụ có chiều cao bằng 10 và bán kính đường tròn đáy bằng 4 là
![]()

![]()
![]()
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt α là góc giữa AB và đáy. Biết rằng thể tích khối tứ diện OO’AB đạt giá trị lớn nhất. Khẳng định nào sau đây đúng?
![]()
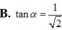
![]()
![]()
Khối trụ tròn xoay có đường cao với bán kính đáy bằng a thì thể tích bằng:
A . a 3
B . π a 3
C . 3 a 3
D . 1 3 π a 3