Khoảng cách giữa hai mặt phẳng ( α ) 2x-y-2z = 0 và ( β ): 2x-y-2z+2=0 là
A. 2
B. 6
C. 10 3
D. 4 3
Những câu hỏi liên quan
Trong không gian Oxyz, khoảng cách giữa mặt phẳng
α
: 2x+4y+4z+10 và mặt phẳng
β
: x+2y+2z+20 bằng A.
3
2
B.
1
3
C.
1
2
D. 1
Đọc tiếp
Trong không gian Oxyz, khoảng cách giữa mặt phẳng α : 2x+4y+4z+1=0 và mặt phẳng β : x+2y+2z+2=0 bằng
A. 3 2
B. 1 3
C. 1 2
D. 1
Tính khoảng cách d giữa hai mặt phẳng song song
(
α
)
:
x
+
2
y
+
2
z
+
11
0
,
(
β
)
:
x
+
2
y
+
2
z
+
2
0
A. d 6 B. d 3 C. d 9 D. d 2
Đọc tiếp
Tính khoảng cách d giữa hai mặt phẳng song song ( α ) : x + 2 y + 2 z + 11 = 0 , ( β ) : x + 2 y + 2 z + 2 = 0
A. d = 6
B. d = 3
C. d = 9
D. d = 2
Trong không gian Oxyz, cho hai mặt phẳng
α
:2x+y-2z+10;
β
:x-2y+2z+30 Tập hợp tất cả các điểm trong không gian cách đều hai mặt phẳng đã cho là A. Một mặt phẳng duy nhất B. Một điểm duy nhất C. Hai mặt phẳng phân biệt vuông góc với nhau D. Một đường thẳng duy nhất song song với cả hai mặt phẳng đã cho
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng α :2x+y-2z+1=0; β :x-2y+2z+3=0 Tập hợp tất cả các điểm trong không gian cách đều hai mặt phẳng đã cho là
A. Một mặt phẳng duy nhất
B. Một điểm duy nhất
C. Hai mặt phẳng phân biệt vuông góc với nhau
D. Một đường thẳng duy nhất song song với cả hai mặt phẳng đã cho
Điểm cần tìm M(x;y;z) ta có điều kiện cách đều hai mặt phẳng là
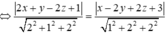
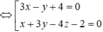
Vậy tập hợp các điểm này nằm trên hai mặt phẳng vuông góc với nhau (hai mặt phẳng này được gọi là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng).
Chọn đáp án C.
Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho hai mặt phẳng
α
:
2
x
+
3
y
-
2
+
2
0
;
β
:
2
x
+
2
y
-
z
+
16
0
. Khoảng cách giữa hai mặt phẳng
α
và
β
là
Đọc tiếp
Cho hai mặt phẳng α : 2 x + 3 y - 2 + 2 = 0 ; β : 2 x + 2 y - z + 16 = 0 . Khoảng cách giữa hai mặt phẳng α và β là
Cho hai mặt phẳng
(
α
)
:
2
x
+
3
y
-
z
+
2
0
,
(
β
)
:
2
x
+
2
y
-
z
+
16
0
. Khoảng cách giữa hai mặt phẳng (α) và (β) là A.
14
B.
23
C. 15 D. 14
Đọc tiếp
Cho hai mặt phẳng ( α ) : 2 x + 3 y - z + 2 = 0 , ( β ) : 2 x + 2 y - z + 16 = 0 . Khoảng cách giữa hai mặt phẳng (α) và (β) là
A. 14
B. 23
C. 15
D. 14
Cho mặt phẳng
α
:
4
x
+
y
+
2
z
+
1
0
và
β
:
2
x
-
2
y
+
z
+
3
0
. Viết phương trình tham số của đường thẳng d là giao của (α) và (β). A.
x...
Đọc tiếp
Cho mặt phẳng α : 4 x + y + 2 z + 1 = 0 và β : 2 x - 2 y + z + 3 = 0 . Viết phương trình tham số của đường thẳng d là giao của (α) và (β).
A. x = t y = 1 - t z = - 1 - 2 t
B. x = t y = 1 z = - 1 - 2 t
C. x = - t y = 1 z = - 1 - 2 t
D. x = - t y = 1 + t z = - 1 - 2 t
Cho mặt phẳng
(
α
)
:
4
x
+
y
+
2
z
+
1
0
và
(
β
)
:
2
x
-
2
y
+
z
-
3
0
. Viết phương trình tham số của đường thẳng d là giao của
α
và
β
Đọc tiếp
Cho mặt phẳng ( α ) : 4 x + y + 2 z + 1 = 0 và ( β ) : 2 x - 2 y + z - 3 = 0 . Viết phương trình tham số của đường thẳng d là giao của α và β
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng
α
:
x
+
y
-
z
+
1
0
v
à
β
:
-
2
x
+
m
y
+
2
z
-
2
0
. Tìm m để mặt phẳng (α) song song với mặt phẳng (β). A. m 2 B. m 5 C. Không tồn tại...
Đọc tiếp
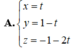
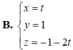
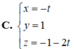
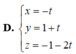
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng α : x + y - z + 1 = 0 v à β : - 2 x + m y + 2 z - 2 = 0 . Tìm m để mặt phẳng (α) song song với mặt phẳng (β).
A. m = 2
B. m = 5
C. Không tồn tại
D. m = -2
Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng α : x+y-z+1=0 và β : -2x+my+2z-2=0. Tìm m để α và β song song
A. Không tồn tại m
B. m=-2
C. m=2
D. m=5
Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0
Viết phương trình tham số của đường thẳng d là giao của (α) và ( β)
