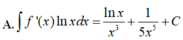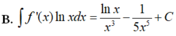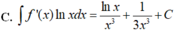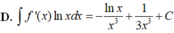Hàm số f ( x ) = x + 3 - a x - b ( x - 1 ) 2 c x > 1 c x ≤ 1 . Để hàm số f(x) liên tục trên R thì giá trị của tổng 2a+b+16c tương ứng bằng
A. 1
B. 0
C. 3
D. 2
Hàm số f(x )có đạo hàm trên R là hàm số f'(x). Biết đồ thị hàm số f'(x), hàm số f(x) nghịch biến trên khoảng:
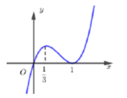
A. 0 ; + ∞
B. 1 3 ; 1
C. - ∞ ; 1 3
D. - ∞ ; 0
Cho hàm số f(x)=1/x. Nếu F(x) là một nguyên hàm của hàm số f(x) và đồ thị hàm số y=F(x) đi qua M(-1;0) thì F(x) là
![]()
![]()
![]()
![]()
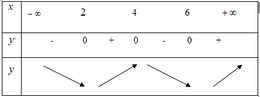
Hàm số f(x) có đạo hàm trên là hàm số f'(x). Biết đồ thị hàm số f'(x) được cho như hình vẽ. Hàm số f(x) nghịch biến trên khoảng
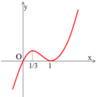
A. 0 ; + ∞
B. 1 3 ; 1
C. − ∞ ; 1 3
D. − ∞ ; 0
Đáp án D
f ' x < 0 ⇔ x < 0 do đó hàm số nghịch biến trên − ∞ ; 0
Cho hàm số y= f(x) . Biết f(x) có đạo hàm f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ.

Hàm số g( x) = f(x- 1) đạt cực đại tại điểm nào dưới đây?
A. x= 2
B. x= 4
C . x= 3
D. x= 1
Chọn B
+ Dựa vào đồ thị hàm số ta thấy :
- Hàm số y= f( x) nghịch biến trên khoảng ( - ∞; 1) và ( 3; 5) .
- Hàm số y= f( x) nghịch biến trên khoảng ( 1 ; 3) và ( 5 ; + ∞)
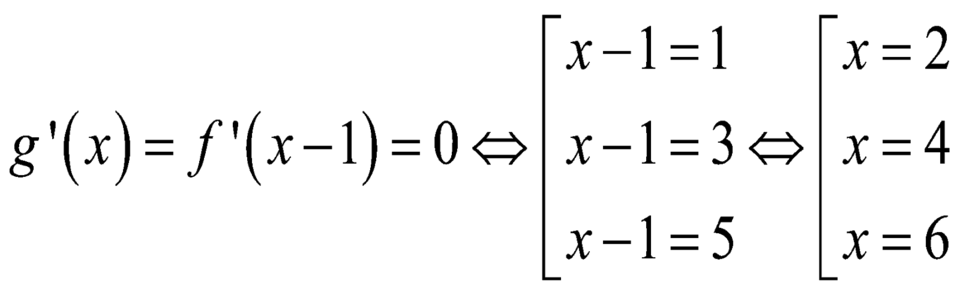
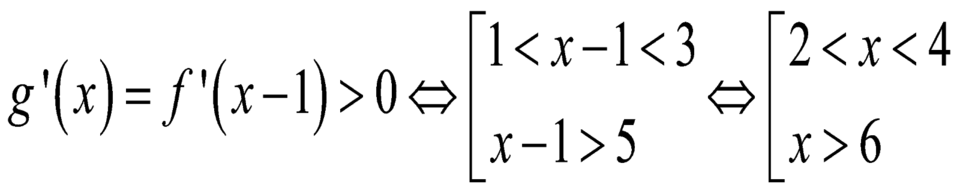
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
Cho hàm số f ( x ) = x 2 ( x - 1 ) e 3 x có một nguyên hàm là hàm số f(x). Số điểm cực trị của hàm số f(x) là
A. 1
B. 2
C. 3
D. 0
Hàm số f(x) có đạo hàm trên R là hàm số f’(x). Biết đồ thị hàm số f’(x)được cho như hình vẽ bên. Hàm số f(x) nghịch biến trên khoảng nào dưới đây?

A. − ∞ ; 0
B. 0 ; + ∞
C. − ∞ ; 1 3
D. 1 3 ; 1
Hàm số f (x) có đạo hàm trên ℝ là hàm số f '(x). Biết đồ thị hàm số f '(x) được cho như hình vẽ bên. Hàm số f (x) nghịch biến trên khoảng nào dưới đây?
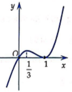
A. - ∞ ; 0
B. 0 ; + ∞
C. - ∞ ; 1 3
D. 1 3 ; 1
Cho F(x) = 1 2 x 2 là 1 nguyên hàm của hàm số f ( x ) x . Tìm nguyên hàm của hàm số f'(x)lnx
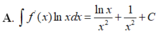
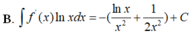
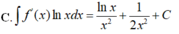
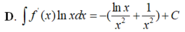
Cho F ( x ) = - 1 3 x 3 là một nguyên hàm của hàm số f ( x ) x Tìm nguyên hàm của hàm số f'(x)lnx