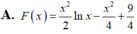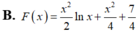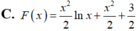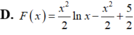Nguyên hàm của hàm số y = 1 x 2 − a 2 (a > 0) là:
A. ∫ 1 x 2 − a 2 d x = 1 a ln x − a x + a + C
B. ∫ 1 x 2 − a 2 d x = 1 2 a ln x − a x + a + C
C. ∫ 1 x 2 − a 2 d x = ln x − a x + a + C
D. ∫ 1 x 2 − a 2 d x = 1 2 a ln x + a x − a + C
Những câu hỏi liên quan
tìm nguyên hàm của hàm số y=x^(2)-3cosx+(1)/(x)
Nguyên hàm của hàm số
y
(
3
x
-
5
)
x
2
-
3
x
+
2
có dạng
a
ln
x
-
1
+
b
ln
x...
Đọc tiếp
Nguyên hàm của hàm số y = ( 3 x - 5 ) x 2 - 3 x + 2 có dạng a ln x - 1 + b ln x - 2 + C Giá trị của a+2b là:
A. 3/2
B. 4
C. 2
D. 4/3
Một nguyên hàm của hàm số
y
2
x
+
2
(
x
+
1
)
2
là A.
ln
(
x
+
1
)
2
B.
ln...
Đọc tiếp
Một nguyên hàm của hàm số y = 2 x + 2 ( x + 1 ) 2 là
A. ln ( x + 1 ) 2
B. ln 2 ( x + 1 )
C. ln ( x 2 + 2 x )
D. ln 2 ( x 2 + 2 x )
Một nguyên hàm của hàm số
y
2
x
+
2
(
x
+
1
)
2
là A.
ln
(
x
+
1
)
2
B.
ln...
Đọc tiếp
Một nguyên hàm của hàm số y = 2 x + 2 ( x + 1 ) 2 là
A. ln ( x + 1 ) 2
B. ln 2 ( x + 1 )
C. ln ( x 2 + 2 x )
D. ln 2 ( x 2 + 2 x )
Một nguyên hàm của hàm số
y
2
x
+
2
(
x
+
1
)
2
là
Đọc tiếp
Một nguyên hàm của hàm số y = 2 x + 2 ( x + 1 ) 2 là
Một nguyên hàm của hàm số
y
2
x
+
2
(
x
+
1
)
2
là A.
ln
(
x
+
1
)
2
B.
ln...
Đọc tiếp
Một nguyên hàm của hàm số y = 2 x + 2 ( x + 1 ) 2 là
A. ln ( x + 1 ) 2
B. ln 2 ( x + 1 )
C. ln ( x 2 + 2 x )
D. ln 2 ( x 2 + 2 x )
Tìm họ nguyên hàm của hàm số
y
1
(
x
+
1
)
2
A.
∫
1
(...
Đọc tiếp
Tìm họ nguyên hàm của hàm số y = = 1 ( x + 1 ) 2
A. ∫ 1 ( x + 1 ) 2 d x = - 2 ( x + 1 ) 3 + C
B. ∫ 1 ( x + 1 ) 2 d x = - 1 x + 1 + C
C. ∫ 1 ( x + 1 ) 2 d x = 1 x + 1 + C
D. ∫ 1 ( x + 1 ) 2 d x = 2 ( x + 1 ) 3 + C
Đáp án B
Phương pháp: Sử dụng công thức ∫ 1 ( a x + b ) 2 = - 1 a ( a x + b ) + C
Cách giải: ∫ 1 ( x + 1 ) 2 d x = - 1 x + 1 + C
Đúng 0
Bình luận (0)
Cho các mệnh đề sau đây:(1) Hàm số
f
(
x
)
log
2
2
x
-
log
2
x
4
+
4
có tập xác định
D
[
0
;
+
∞
)
(2) Hàm số
y
log
a
x
có tiệm cận ngang(3) Hàm số
y
log
a
x
;
...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Cho hàm số \(y=x^2+2x+3+\left|x-a+1\right|\), có bao nhiêu giá trị nguyên của tham số a \(\in\left[-10;10\right]\) sao cho giá trị nhỏ nhất của hàm số lớn hơn 2
Tìm một nguyên hàm F(x) của hàm số y=f(x)=xlnx, (x>0) biết rằng F(1)=2.
