Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 2 x - 4 y + 6 ≥ 1 , tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 13 - 3 v à 13 + 3
B. 13 - 3
C. 13 - 3 2
D. 13 - 3 2 và 13 + 3 2
Những câu hỏi liên quan
Biết rằng trong tất cả các cặp (x; y) thỏa mãn:
log
2
x
2
+
y
2
+
2
≤
log
2
x
+
y
-
1...
Đọc tiếp
Biết rằng trong tất cả các cặp (x; y) thỏa mãn: log 2 x 2 + y 2 + 2 ≤ log 2 x + y - 1 . Chỉ có duy nhất một cặp (x; y) thỏa mãn: 3x + 4y - m = 0 . Khi đó hãy tính tổng tất cả các giá trị m tìm được?
A. 20
B. 46
C. 28
D. 14
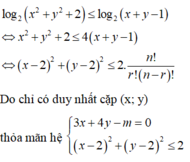
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
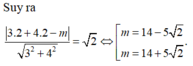
Chọn C.
Đúng 0
Bình luận (0)
Biết rằng trong tất cả các cặp (x;y) thỏa mãn
log
2
x
2
+
y
2
+
2
≤
log
2
x
+
y
-
1
chỉ có duy nhất một cặp (x;y) thỏa mãn 3x+4y-m0....
Đọc tiếp
Biết rằng trong tất cả các cặp (x;y) thỏa mãn log 2 x 2 + y 2 + 2 ≤ log 2 x + y - 1 chỉ có duy nhất một cặp (x;y) thỏa mãn 3x+4y-m=0. Khi đó hãy tính tổng tất cả các giá trị m tìm được.
A. 20
B. 28
C. 46
D. 14
Biết rằng trong tất cả các cặp (x; y) thỏa mãn:
log
2
x
2
+
y
2
+
2
≤
2
+
log
2
x
+
y
-
1
. Chỉ có duy nhất một cặp (x;...
Đọc tiếp
Biết rằng trong tất cả các cặp (x; y) thỏa mãn: log 2 x 2 + y 2 + 2 ≤ 2 + log 2 x + y - 1 . Chỉ có duy nhất một cặp (x; y) thỏa mãn: 3x + 4y - m = 0 . Khi đó hãy tính tổng tất cả các giá trị m tìm được?
A. 20
B. 46
C. 28
D. 14
Câu 18(TH): Thể ba nhiễm (hay tam nhiễm) là thể mà trong tế bào sinh dưỡng có:A. tất cả các cặp NST tương đồng đều có 3 chiếcB. tất cả các cặp NST tương đồng đều có 1 chiếcC. tất cả các cặp NST tương đồng đều có 2 chiếcD. một cặp NST nào đó có 3 chiếc, các cặp còn lại đều có 2 chiếcCâu 19(TH): Kí hiệu bộ NST nào sau đây dùng để chỉ có thể không nhiễm?A. 2n + 1 B. 2n – 1 C. 2n + 2 D. 2n – 2Câu 20(NB): Thể dị bội có thể tìm thấy ở loài nào sau đây?A. Ruồ...
Đọc tiếp
Câu 18(TH): Thể ba nhiễm (hay tam nhiễm) là thể mà trong tế bào sinh dưỡng có:
A. tất cả các cặp NST tương đồng đều có 3 chiếc
B. tất cả các cặp NST tương đồng đều có 1 chiếc
C. tất cả các cặp NST tương đồng đều có 2 chiếc
D. một cặp NST nào đó có 3 chiếc, các cặp còn lại đều có 2 chiếc
Câu 19(TH): Kí hiệu bộ NST nào sau đây dùng để chỉ có thể không nhiễm?
A. 2n + 1 B. 2n – 1 C. 2n + 2 D. 2n – 2
Câu 20(NB): Thể dị bội có thể tìm thấy ở loài nào sau đây?
A. Ruồi giấm
B. Đậu Hà Lan
C. Người
D. Ruồi giấm, đậu Hà Lan, người.
Câu 21(VD): Một loài sinh vật có 2n= 20. Bộ NST của thể tam bội chứa số NST là:
A. 10 B. 20 C. 30 D. 21
Câu 22(VD): Ở đậu Hà Lan có 2n = 14. Dự đoán số lượng NST trong tế bào sinh dưỡng ở thể dị bội là bao nhiêu?
A. 16 B. 21 C. 28 D. 35
Câu 23(VD): Số NST trong tế bào là thể 3 nhiễm ở người là:
A. 47 chiếc NST C. 45 chiếc NST
B. 47 cặp NST D. 45 cặp NST
Câu 24(VD): Bệnh Đao có ở người xảy ra là do trong tế bào sinh dưỡng:
A. Có 3 NST ở cặp số 12 C. Có 3 NST ở cặp số 21
B. Có 1 NST ở cặp số 12 D. Có 3 NST ở cặp giới tính.
Câu 18(TH): Thể ba nhiễm (hay tam nhiễm) là thể mà trong tế bào sinh dưỡng có:
A. tất cả các cặp NST tương đồng đều có 3 chiếc
B. tất cả các cặp NST tương đồng đều có 1 chiếc
C. tất cả các cặp NST tương đồng đều có 2 chiếc
D. một cặp NST nào đó có 3 chiếc, các cặp còn lại đều có 2 chiếc
Câu 19(TH): Kí hiệu bộ NST nào sau đây dùng để chỉ có thể không nhiễm?
A. 2n + 1 B. 2n – 1 C. 2n + 2 D. 2n – 2
Câu 20(NB): Thể dị bội có thể tìm thấy ở loài nào sau đây?
A. Ruồi giấm
B. Đậu Hà Lan
C. Người
D. Ruồi giấm, đậu Hà Lan, người.
Câu 21(VD): Một loài sinh vật có 2n= 20. Bộ NST của thể tam bội chứa số NST là:
A. 10 B. 20 C. 30 D. 21
Câu 22(VD): Ở đậu Hà Lan có 2n = 14. Dự đoán số lượng NST trong tế bào sinh dưỡng ở thể dị bội là bao nhiêu?
A. 16 B. 21 C. 28 D. 35
Câu 23(VD): Số NST trong tế bào là thể 3 nhiễm ở người là:
A. 47 chiếc NST C. 45 chiếc NST
B. 47 cặp NST D. 45 cặp NST
Câu 24(VD): Bệnh Đao có ở người xảy ra là do trong tế bào sinh dưỡng:
A. Có 3 NST ở cặp số 12 C. Có 3 NST ở cặp số 21
B. Có 1 NST ở cặp số 12 D. Có 3 NST ở cặp giới tính.
Đúng 2
Bình luận (0)
1)Tim tất cả các cặp số nguyên x,y thỏa mãn :(x+5)y-x=10
2)Tìm tất cả các cặp số nguyên c,d để tích của chúng bằng 5 lần tổng của chúng
tớ chỉ làm phần 1 thôi
1. ta có (x+5)y-x=10
=>(x+5)y-x-5=10-5
=>(x+5)y-(x+5)=5
=>(x+5)(y-1)=5
lập bảng xét giá trị của x,y \(\in Z\)
Bạn tự làm tiếp nhé -_-
Đúng 2
Bình luận (0)
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m để tồn tại duy nhất cặp (x;y) sao cho
x...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 10 - 2 2
B. 10 - 2 h o ặ c 10 + 2
C. 10 - 2 2 h o ặ c 10 + 2 2
D. 10 - 2
Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
Đúng 0
Bình luận (0)
Trong tất cả các cặp (x;y) thỏa mãn
l
o
g
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
Tìm m để tồn tại duy nhất cặp (x;y) sao cho...
Đọc tiếp
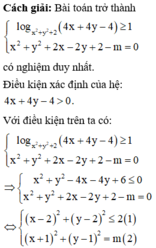
Trong tất cả các cặp (x;y) thỏa mãn l o g x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 Tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m n...
Đọc tiếp
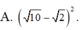
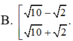
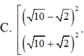
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 10 - 2 2
B. 10 + 2
C. 10 + 2 2
D. 10 - 2
log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1
⇔ 4 x + 4 y - 4 ≥ x 2 + y 2 + 2 ⇔ x - 2 2 + y - 2 2 ≤ 2
Đây là tập hợp tất cả các điểm nằm trên và trong đường tròn tâm I(2;2) bán kính ℝ ' = m .
Ta có I I ' = 10 . m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 thì hai đường tròn nói trên tiếp xúc ngoài
⇒ R + R ' = I I ' ⇔ m + 2 = 10 ⇔ m = 10 - 2 2
Đáp án cần chọn là B
Đúng 0
Bình luận (0)
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0
A. 10 - 2 2
B. 10 + 2
C. 10 + 2 2
D. 10 - 2