Cho tứ diện đều ABCD. Góc giữa hai đường thằng AB và CD là
A. 60 °
B. 90 °
C. 45 °
D. 30 °
Những câu hỏi liên quan
Cho tứ diện đều ABCD Góc giữa hai đường thằng AB và CD là A.
60
0
.
B.
90
0
.
C.
45
0
.
D.
30
0
.
Đọc tiếp
Cho tứ diện đều ABCD Góc giữa hai đường thằng AB và CD là
A. 60 0 .
B. 90 0 .
C. 45 0 .
D. 30 0 .
Cho tứ diện đều ABCD đều có cạnh bằng a
a) tính góc giữa hai đường thẳng AB và CD ,AD và BC
b) tính góc giữa các vectơ AC và AB ,AC VÀ DA
Xem chi tiết
Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD là
A. 45⁰.
B. 90⁰.
C. 60⁰.
D. 30⁰.
Cho tứ diện ABCD có BCa,
C
D
a
3
,
B
C
D
^
A
B
C
^
A
D
C
^
90
°
. Góc giữa hai đường thẳng AD và BC bằng
60
°...
Đọc tiếp
Cho tứ diện ABCD có BC=a, C D = a 3 , B C D ^ = A B C ^ = A D C ^ = 90 ° . Góc giữa hai đường thẳng AD và BC bằng 60 ° . Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD.
A. a 3 2
B. a 3
C. a
D. a 7 2
Cho tứ diện ABCD có BC 3, CD 4,
B
C
D
⏜
A
B
C
⏜
A
D
C
⏜
90
°
. Góc giữa hai đường thẳng AD và BC bằng
60
°
. Tính thể tích khối cầu ngoại tiếp tứ diện ABCD A. ...
Đọc tiếp
Cho tứ diện ABCD có BC = 3, CD = 4, B C D ⏜ = A B C ⏜ = A D C ⏜ = 90 ° . Góc giữa hai đường thẳng AD và BC bằng 60 ° . Tính thể tích khối cầu ngoại tiếp tứ diện ABCD
A. 127 127 π 6
B. 52 13 π 3
C. 28 7 π 3
D. 32 3 π
Cho tứ diện đều ABCD. Góc giữa hai đường thẳng AB và CD bằng
A. 600
B. 900
C. 450
D. 300
Đáp án B
Phương pháp giải: Tứ diện đều có cặp cạnh đối vuông góc với nhau
Lời giải:
Gọi M là trung điểm của CD. Hai tam giác ACD, BCD đều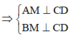 
Vậy góc giữa hai đường thẳng AB và CD bằng 900
Đúng 0
Bình luận (0)
Cho tứ diện đều ABCD. Góc giữa hai đường thẳng AB và CD bằng
Cho tứ diện đều ABCD. Góc giữa hai đường thẳng AB và CD bằng:
A. 60°
B. 90°
C. 45°
D. 30°
Đáp án B.
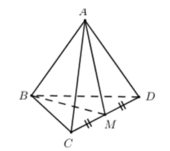
- Phương pháp: Tứ diện đều có các cặp cạnh đối vuông góc.
- Cách giải:
+ Gọi M là trung điểm của CD ta có:
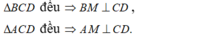
+ Ta có:
Đúng 1
Bình luận (0)
Cho khối tứ diện ABCD có
B
C
3
,
C
D
4
,
A
B
C
^
B
C
D
^
A
D
C
^
90
°
Góc giữa hai đường thẳng AD...
Đọc tiếp
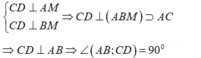
Cho khối tứ diện ABCD có B C = 3 , C D = 4 , A B C ^ = B C D ^ = A D C ^ = 90 ° Góc giữa hai đường thẳng AD và BC bằng 60 ° Côsin góc giữa hai mặt phẳng (ABC) và (ACD) bằng
A. 2 43 43
B. 43 86
C. 4 43 43
D. 43 43
