Hàm số nào sau đây có một nguyên hàm là đạo hàm của hàm số y = sin2x?
![]()
![]()
![]()
![]()
Hàm số nào sau đây có một nguyên hàm là đạo hàm của hàm số y=sin2x
A. y=sin2x
B. y=cos2x
C. y=-4sin2x
D. y=4sin2x
Hàm số y=cos x. sin2x có đạo hàm là biểu thức nào sau đây
![]()
![]()
![]()
![]()
Đạo hàm của hàm số y = cos6x + sin4x. cos2x + sin2x. cos4x + sin4x – sin2x bằng biểu thức nào sau đây?
A. - 6 cos 5 x sin x
B. 6 cos 5 x sin x
C. 6 sin 5 x cos x
D. 6 cos 5 x
Chọn A
y = cos6 x+ sin2xcos2x(sin2x + cos2x) + sin4x - sin2x
= cos6x + sin2x(1 - sin2x) + sin4x - sin2x = cos6x
Do đó : y' = -6cos5xsinx.
Đạo hàm cấp 4 của hàm số y = sin 2 x bằng biểu thức nào sau đây?
A. 2 4 sin 2 x + 4 π 2
B. 2 3 sin 2 x + 4 π 2
C. 2 3 sin 2 x - 3 π 2
D. 2 3 sin 2 x + 3 π 2
Đạo hàm của hàm số: y = sin 2 x + cos x 2 + 1 2 - tan x bằng biểu thức nào sau đây?
A. cos 2 x - sin x 2 + 1 2 - 1 cos 2 x
B. 2 cos 2 x - x sin x 2 + 1 2 - 1 2 x cos 2 x
C. - 2 cos x + x sin x 2 + 1 2 - 1 2 x cos 2 x
D. 2 cos 2 x + x sin x 2 + 1 2 - 1 2 x cos 2 x
y ' = c os2x. (2x)' - sin x + 2 1 2 . x + 2 1 2 ' − 1 cos 2 x . ( x ) '
![]()
Chọn B
Trong các hàm số sau, hàm số nào là một nguyên hàm của hàm f x = sin 2 x ?
A. y = 1 2 x − sin 2 x .
B. y = 1 2 x − 1 4 sin 2 x
C. y = 1 2 x + sin 2 x .
D. y = 1 2 x + 1 4 sin 2 x .
Trong các cặp hàm số dưới đây, hàm số nào là nguyên hàm của hàm số còn lại? sin 2 x v à sin sin 2 x
Tìm khẳng định sai trong các khẳng định sau đây:
A. Hàm số y = 4cosx - 5 sin 2 x - 3 là hàm số chẵn;
B. Đồ thị hàm số sau có hai tiệm cận đứng
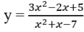
C. Hàm số 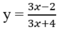 luôn nghịch biến;
luôn nghịch biến;
D. Hàm số
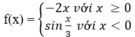
không có đạo hàm tại x = 0.
Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 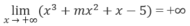
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.
Tìm khẳng định sai trong các khẳng định sau đây:
A. Hàm số y = 4cosx - 5 sin 2 x - 3 là hàm số chẵn;
B. Đồ thị hàm số sau có hai tiệm cận đứng y = 3 x 2 - 2 x + 5 x 2 + x - 7
C. Hàm số y = 3 x - 2 3 x + 4 luôn nghịch biến;
D. Hàm số f x = - 2 x với x ≥ 0 sin x 3 với x < 0
không có đạo hàm tại x = 0.
Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 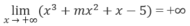
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.