Cho hình nón đỉnh (S) có đường sinh bằng 3 , đường cao bằng 1 . Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho:
![]()
![]()
![]()
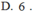
Cho hình nón đỉnh (S) có đường sinh bằng 2 , đường cao bằng 1 . Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho:
![]()
![]()
![]()
![]()
Cho hình nón đỉnh S có đường sinh bằng 2, đường cao bằng 1. Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho
A. 4
B. 2
C. 1
D. 2 3
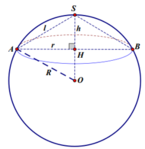
Gọi O, R lần lượt là tâm và bán kính của mặt cầu.
Đường tròn đáy của hình nón có tâm H bán kính r.
Do H là hình chiếu của S và O trên mặt đáy của hình nón nên S, H, O thẳng hàng.
Hình nón có độ dài đường sinh l=2, đường cao h=1.
Suy ra r = l 2 - h 2 = 3
Góc ở đỉnh của hình nón là A S B = 2 A S H = 120 ° nên suy ra H ∈ S O (như hình vẽ).
Trong tam giác OAH vuông tại H ta có:
O A 2 = O H 2 + H A 2 ⇔ R 2 = R - h 2 + r 2 ⇔ R = h 2 + r 2 2 h = 2
Vậy đường kính mặt cầu chứa điểm S và đường tròn đáy hình nón bằng 4.
Chọn đáp án A.
Cách 2:
Gọi O, R lần lượt là tâm và bán kính của mặt cầu.
Đường tròn đáy của hình nón có tâm H bán kính r.
Do H là hình chiếu của S và O trên mặt đáy của hình nón nên S, H, O thẳng hàng.
Hình nón có độ dài đường sinh l=2, đường cao h=1. (như hình vẽ)
Trong tam giác SAH vuông tại H ta có
cos A S H = S H S A = 1 2 ⇒ A S H = 60 °
Xét tam giác SOA có OS=OA=R và O S A = 60 °
Suy ra tam giác SOA đều.
Do đó R=OA=SA=2
Vậy đường kính mặt cầu chứa điểm S và đường tròn đáy hình nón bằng 4.
Chọn đáp án A.
Cho hình nón đỉnh S có đường sinh bằng 2, đường cao bằng 1. Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho
A. 4
B. 2
C. 1
D. 2 3
Cho hình nón đỉnh S có đường sinh bằng 2, đường cao bằng 1. Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho.
A. 4
B. 2
C. 1
D. 2 3
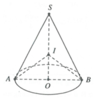
HD: Ta có tâm I của mặt cầu chính là tâm đường tròn ngoại tiếp tam giác SAB.

Cho hình nón có đường sinh bằng 2 và diện tích xung quanh bằng 2 3 π . Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho
![]()
![]()
![]()
![]()
Cho một hình nón đỉnh S có chiều cao bằng 8cm, bán kính đáy bằng 6cm. Cắt hình nón đã cho bởi một mặt phẳng song song với mặt phẳng chứa đáy được một hình nón (N) đỉnh S có đường sinh bằng 4cm. Tính thể tích của khối nón (N).
A. 768 125 π cm 3
B. 786 125 π cm 3
C. 2304 125 π cm 3
D. 2358 125 π cm 3
Cho hình nón đỉnh S, đường tròn đáy tâm O bán kính r=3, đường cao SO=3. Mặt phẳng (P) di động luôn vuông góc với SO tại điểm H (nằm giữa S và O) cắt mặt nón theo giao tuyến là đường tròn (C). Mặt cầu (T) chứa (C) và tiếp xúc với đáy hình nón tại O. Thể tích khối cầu (T) đạt min =?
- Nếu H nằm ở nửa dưới đoạn SO thì \(R\ge\dfrac{SO}{2}=\dfrac{3}{2}\)
- Nếu H nằm ở nửa trên đoạn SO, thực hiện mặt cắt qua trục nón như hình vẽ
\(SO=OA=3\Rightarrow SOA\) vuông cân \(\Rightarrow SCH\) vuông cân
\(\Rightarrow CH=SH=3-OH=3-\left(R+IH\right)=3-R-\sqrt{R^2-CH^2}\)
\(\Rightarrow3-R=CH+\sqrt{R^2-CH^2}\le\sqrt{2\left(CH^2+R^2-CH^2\right)}=R\sqrt{2}\)
\(\Rightarrow R\left(\sqrt{2}+1\right)\ge3\Rightarrow R\ge\dfrac{3}{\sqrt{2}+1}=3\left(\sqrt{2}-1\right)\)
\(V_{min}=\dfrac{4}{3}\pi R_{min}^3=8,037\)
Cho S : x 2 + y - 1 2 + z + 1 2 = 8 và A 2 ; 3 ; - 1 . Xét mặt nón tròn xoay đỉnh A trục là IA( I là tâm mặt phẳng (S)) với góc ở đỉnh bằng 120 0 , đường tròn đáy hình nón thuộc mặt cầu. Viết phương trình mặt phẳng (P) chứa đường tròn đáy hình nón.
![]()
![]()
![]()
![]()
Cho hình nón đỉnh S có chiều cao h = a và bán kính đáy r = 2a. Mặt phẳng (P) đi qua S, không chứa trục của hình nón cắt đường tròn đáy tại A và B sao cho AB = 2 3 a .Khoảng cách từ âm của hình tròn đáy đến mặt phẳng (P) bằng

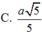
![]()