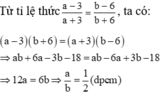Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)

\(\left(\frac{a+b}{c+d}\right)^3=\left(\frac{bk+b}{dk+d}\right)^3=\left(\frac{b\left(k+1\right)}{d\left(k+1\right)}\right)^3=\left(\frac{b}{d}\right)^3\left(1\right)\)

\(\frac{a^3+b^3}{c^3+d^3}=\frac{\left(bk\right)^3+b^3}{\left(dk\right)^3+d^3}=\frac{b^3k^3+b^3}{d^3k^3+d^3}=\frac{b^3\left(k^3+1\right)}{d^3\left(k^3+1\right)}=\frac{b^3}{d^3}=\left(\frac{b}{d}\right)^3\left(2\right)\)

Từ (1) & (2)=>\(\left(\frac{a+b}{c+d}\right)^3=\frac{a^3+b^3}{c^3+d^3}\)

CMR \(\frac{a-b}{a}=\frac{c-d}{c}\)

gọi giá trị chung của \(\frac{a}{b}=\frac{c}{d}=k\)

=> \(a=k.b;c=k.d\)

Ta có

  \(\frac{a-b}{a}=\frac{k.b-b}{k.b}=\frac{b.\left(k-1\right)}{k.b}=\frac{k-1}{k}\)

 \(\frac{c-d}{c}=\frac{k.d-d}{k.d}=\frac{d.\left(k-1\right)}{k.d}=\frac{k-1}{k}\)

 Vì \(\frac{k-1}{k}=\frac{k-1}{k}\)

=> \(\frac{a-b}{a}=\frac{c-d}{c}\)

Gọi giá trị chung của hai tỉ số đó là k, ta có :

\(\frac{a}{b}=\frac{c}{d}=k\)

\(\Rightarrow a=k\times b\)  ;  \(c=k\times d\)

Ta có :

\(\frac{a-b}{a}=\frac{k\times b-b}{k\times b}=\frac{b\times\left(k-1\right)}{k\times b}=\frac{k-1}{k}\)        (1)
\(\frac{c-d}{c}=\frac{k\times d-d}{k\times d}=\frac{d\times\left(k-1\right)}{k\times d}=\frac{k-1}{k}\)         (2)

Từ (1) và (2) \(\Rightarrow\) \(\frac{a-b}{a}=\frac{c-d}{c}\)

Theo bài ra ta có: a,b tỉ lệ thuận với 2,3

Suy ra: a/2=b/3 

Suy ra a/4=b/6 (1)

b,c tỉ lệ nghịch với 3,2

Suy ra: b.3=c.2 

Suy ra b/2=c/3

Suy ra: b/6=c/9 (2) 

Từ (1) và (2) ta có: a/4=b/6=c/9

Lại có a+b+c=38

áp dụng tính chất dãy tỉ số bằng nhau ta được:

a/4=b/6=c/9=(a+b+c)/(4+6+9)=38/19=2

Do đó: a/4=2 suy ra a=2.4=8

b/6=2 suy ra b=2.6=12

c/9=2 suy ra c=2.9=18

Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)

\(\frac{a^2-b^2}{ab}=\frac{\left(bk\right)^2-b^2}{bk.b}=\frac{b^2.k^2-b^2}{b^2k}=\frac{b^2\left(k^2-1\right)}{b^2k}=\frac{k^2-1}{k}\left(1\right)\)

\(\frac{c^2-d^2}{cd}=\frac{\left(dk\right)^2-d^2}{dk.d}=\frac{d^2k^2-d^2}{d^2k}=\frac{d^2\left(k^2-1\right)}{d^2.k}=\frac{k^2-1}{k}\left(2\right)\)

Từ (1) và (2)=>\(\frac{a^2-b^2}{ab}=\frac{c^2-d^2}{cd}\).

phần b đề kiểu gì vậy??//

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)

=>\(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)

Ta có:\(\left(\dfrac{a+b}{c+d}\right)^3=\left(\dfrac{bk+b}{dk+d}\right)^3=\left(\dfrac{b.\left(k+1\right)}{d.\left(k+1\right)}\right)^3=\dfrac{b^3}{d^3}\)(1)

Lại có :\(\dfrac{a^3+b^3}{c^3+d^3}=\dfrac{b^3k^3+b^3}{d^3k^3+d^3}=\dfrac{b^3.\left(k^3+1\right)}{d^3.\left(k^3+1\right)}=\dfrac{b^3}{d^3}\)(2)

Từ (1) và (2) => ĐPCM

Từ a/b=c/d

=>a/c=b/d=a+b/c+d

<=>a^3/c^3=b^3/d^3=(a+b)^3(c+d)^3

=a^3+b^3/c^3+d^3

Vậy

(a+b)^3(c+d)^3=a^3+b^3/c^3+d^3 (đpcm)

A

a

A