Hệ thức liên hệ giữa giá trị cực đại và giá trị cực tiểu của hàm số y = x 3 - 2 x là:
A. y C T + y C D = 0
B. y C T = y C D
C. 2 y C T = 3 y C D
D. y C D = 2 y C T
Những câu hỏi liên quan
Hệ thức liên hệ giữa giá trị cực đại
y
C
D
và giá trị cực tiểu
y
C
T
của đồ thị hàm số
y
x
3
-
2
x
là: A.
y
C
D
+
y
C
T...
Đọc tiếp
Hệ thức liên hệ giữa giá trị cực đại y C D và giá trị cực tiểu y C T của đồ thị hàm số y = x 3 - 2 x là:
A. y C D + y C T = 0
B. y C T = 2 y C D
C. y C T = y C D
D. 2 y C T = 3 y C D
Đáp án A
Xét hàm số y = x 3 - 2 x , ta có y ' = 3 x 2 - 2 ; y ' ' = 6 x
Phương trình
y ' = 0 ⇔ x 2 = 2 3 ⇔ x = ± 6 3 ⇒ y C T = - 4 6 9 y C D = 4 6 9 ⇒ y C T + y C D = 0
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
+
3
x
2
-
1
. Biểu thức liên hệ giữa giá trị cực đại
y
C
N
~
và giá trị cực tiểu
y
C
T
là A.
y...
Đọc tiếp
Cho hàm số y = x 3 + 3 x 2 - 1 . Biểu thức liên hệ giữa giá trị cực đại y C N ~ và giá trị cực tiểu y C T là
A. y C N ~ = 3 y C T
B. y C T = - 3 y C N ~
C. y C N ~ = - y C T
D. y C N ~ = - 3 y C T
Cho hàm số
y
x
3
+
3
x
2
−
1
. Biểu thức liên hệ giữa giác trị cực đại
y
CÑ
và giá trị cực tiểu
y
CT
là: A.
y
CÑ
3
y
CT
B.
y...
Đọc tiếp
Cho hàm số y = x 3 + 3 x 2 − 1 . Biểu thức liên hệ giữa giác trị cực đại y CÑ và giá trị cực tiểu y CT là:
A. y CÑ = 3 y CT
B. y CT = − 3 y CÑ
C. y CÑ = − y CT
D. y CÑ = − 3 y CT
Đáp án D
Ta có y ' = 3 x 2 + 6 x = 3 x x + 2 ⇒ y ' = 0 ⇔ x = 0 x = − 2
Hàm số đạt cực đại tại x = − 2 ⇒ y C D = 3
Hàm số đạt cực tiểu tại x = 0 ⇒ y C T = − 1
Đúng 0
Bình luận (0)
Cho hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
đạt cực đại tại x -2 với giá trị cực đại là 64; đạt cực tiểu tại x 3 với giá trị cực tiểu là -61. Khi đó giá trị của a + b + c + d bằng A. 1 B. 7 C. -17 D. 5
Đọc tiếp
Cho hàm số y = a x 3 + b x 2 + c x + d đạt cực đại tại x = -2 với giá trị cực đại là 64; đạt cực tiểu tại x = 3 với giá trị cực tiểu là -61. Khi đó giá trị của a + b + c + d bằng
A. 1
B. 7
C. -17
D. 5
Ta có 64 = -8a + 4b - 2c + d; -61 = 27a + 9b + 3c +d
Từ y ' = 3 a x 2 + 2 b x + c ta thu được hai phương trình 0 = 12a - 4b + c; 0 = 27a + 6b + c
Giải hệ gồm 4 phương trình trên ta thu được a = 2; b = -3; c = -36; d = 20 hay a + b + c + d = -17
Đáp án C
Đúng 0
Bình luận (0)
Hiệu số giữa giá trị cực đại và giá trị cực tiểu của hàm số
y
x
3
−
3
x
2
+
2
là A. 4 B. -4 C. 2 D. -2
Đọc tiếp
Hiệu số giữa giá trị cực đại và giá trị cực tiểu của hàm số y = x 3 − 3 x 2 + 2 là
A. 4
B. -4
C. 2
D. -2
Đáp án A
TXĐ: D = ℝ .
y ' = 3 x 2 − 6 x = 0 ⇔ 3 x x − 2 = 0 ⇔ x = 0 x = 2 .
Ta có bảng biến thiên
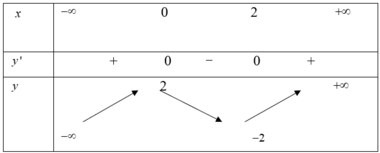
Vậy hiệu số giữa giá trị cực đại và giá trị cực tiểu của hàm số là 4.
Đúng 0
Bình luận (0)
Hiệu số giữa giá trị cực đại và giá trị cực tiểu của hàm số
y
x
3
-
3
x
2
+
4
là A. 4 B. -2 C. 2 D. -4
Đọc tiếp
Hiệu số giữa giá trị cực đại và giá trị cực tiểu của hàm số y = x 3 - 3 x 2 + 4 là
A. 4
B. -2
C. 2
D. -4
Cho hàm số y f(x) xác định, liên tục trên R và có bảng biến thiên như sau:Tìm giá trị cực đại
y
C
Đ
và giá trị cực tiểu
y
C
T
của hàm số đã cho. A.
y
C
Đ
−
2
v
à
y
C...
Đọc tiếp
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
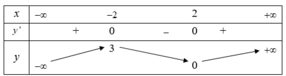
Tìm giá trị cực đại y C Đ và giá trị cực tiểu y C T của hàm số đã cho.
A. y C Đ = − 2 v à y C T = 2
B. y C Đ = 3 v à y C T = 0
C. y C Đ = 2 v à y C T = 0
D. y C Đ = 3 v à y C T = - 2
Phương pháp:
Quan sát bảng biến thiên và tìm điểm cực đại, cực tiểu và các giá trị cực đại, cực tiểu tương ứng.
Cách giải:
Số cách chọn là: 6.4 = 24 (cách). Quan sát bảng biến thiên ta thấy:
Hàm số đạt cực đại tại x = 2 và yCD = 3 .
Hàm số đạt cực tiểu tại x = 2 và yCT = 0 .
Vậy yCD = 3 và yCT = 0 .
Chọn: B
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có bảng biến thiên như sau:Giá trị cực đại và giá trị cực tiểu của hàm số đã cho lần lượt là? A. 3 và -2 B. 2 và 0 C. -2 và 2 D. 3 và 0
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như sau:
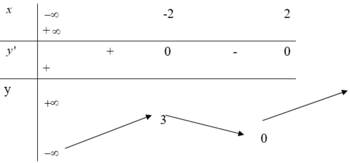
Giá trị cực đại và giá trị cực tiểu của hàm số đã cho lần lượt là?
A. 3 và -2
B. 2 và 0
C. -2 và 2
D. 3 và 0
Giá trị cực đại bằng y(-2)=3 giá trị cực tiểu bằng y(2)=0
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
3
x
2
-
2
. Gọi a,b lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số đó. Giá trị của
2
a
2
+
b
là...
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 - 2 . Gọi a,b lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số đó. Giá trị của 2 a 2 + b là:
A. -8.
B. -2
C. 2
D. 4
Chọn C
y ' = 3 x 2 - 6 x
y ' = 0 ⇔ x = 0 x = 2
Đúng 0
Bình luận (0)