Cho hình hộp A B C D . A ' B ' C ' D ' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 ∘ . Tính khoảng cách giữa hai đường thẳng A B ' v à A ' C '
A. 22 11
B. 2 11
C. 2 11
D. 3 11
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 o . Tính khoảng cách giữa hai đường thẳng AB' và A' C'
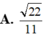
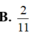
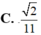
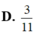
Cho khối hộp ABCD.A′B′C′D′ có tất cả các cạnh bằng 2a, có đáy là hình vuông và cạnh bên tạo với mặt phẳng đáy khối hộp một góc bằng 60 o Thể tích khối hộp bằng
A. 8 a 3
B. 2 3 a 3
C. 8 3 a 3
D. 4 3 a 3
Cho khối hộp ABCD.A′B′C′D′ có tất cả các cạnh bằng 2a, có đáy là hình vuông và cạnh bên tạo với mặt phẳng đáy khối hộp một góc bằng 60 ° . Thể tích khối hộp bằng
A. 8 a 3
B. 2 3 a 3
C. 8 3 a 3
D. 4 3 a 3
Câu 2. Cho hình hộp thoi ABCD.A'B'C'D' có tất cả các cạnh bằng a và các góc ABC = B'BA = B'BC = 60o. Chứng minh tứ giác A'B'CD là hình vuông.
Câu 3. Cho hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a và các góc BAD, DAA' , A'AB đều bằng 60o . Gọi M, N lần lượt là trung điểm của AA' , CD. Gọi α là góc tạo bởi hai đường thẳng MN và B'C. Tính cos α
Câu 4. Cho hình chóp S.ABCD, có đáy ABCD là hình vuông tâm O, cạnh bằng a; SA vuông góc với đáy và SA = a√3. Khi đó, cosin góc giữa SB và AC bằng
cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng a. góc BAA'= góc BAD = góc DAA' = 60 độ. tính độ dài AC'?
Do tất cả các cạnh bằng a nên các mặt bên đều là hình thoi.
Mà \(\widehat{BAA'}=\widehat{BAD}=\widehat{DAA'}=60^0\Rightarrow A'B=A'D=AA'=BD=a\)
\(\Rightarrow\) Hình chiếu vuông góc H của A' lên (ABCD) là tâm tam giác đều ABD
\(AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\) ; \(AC=a\sqrt{3}\)
\(cos\widehat{A'AC}=\dfrac{AH}{AA'}=\dfrac{\sqrt{3}}{3}\Rightarrow cos\widehat{ACC'}=-\dfrac{\sqrt{3}}{3}\)
Áp dụng định lý hàm cos cho tam giác ACC':
\(AC'=\sqrt{AC^2+C'C^2-2AC.C'C.cos\widehat{ACC'}}=a\sqrt{6}\)
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 0 . Tính khoảng cách giữa hai đường thẳng AB' và A'C'
A . 22 11
B . 2 11
C . 2 11
D . 3 11
Đáp án A.
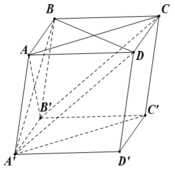
Ta có AA'BC là chóp đều có tất cả các cạnh bằng 1
![]()
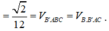
Ta có ![]()
![]()
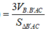
Lại có
∆
AB'C có B'C = A'D = 1; ![]() (do là hình thoi cạnh 1 có
B
A
D
^
=
60
0
)
(do là hình thoi cạnh 1 có
B
A
D
^
=
60
0
)
Do đó
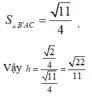
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 ° . Tính khoảng cách giữa hai đường thẳng AB' và A'C'
A. 22 11
B. 2 11
C. 2 11
D. 3 11
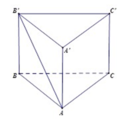
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Tang của góc giữa đường thẳng AB′ và mặt phẳng (ACC′A′) bằng
A. 1.
B. 15 5
C. 15 3
D. 6 2
Cho khối hộp ABCD.A′B′C′D′ có tất cả các cạnh bằng 1. Các góc tại đỉnh A bằng 60 ° . Khoảng cách giữa hai đường thẳng BD và AC′ bằng
A. 6 6
B. 2 6
C. 3 6
D. 3 12