Biết rằng ∫ e 2 x cos 3 xdx = e 2 x a cos 3 x + b sin 3 x + c , trong đó a, b, c là các hằng số, khi đó tổng a + b có giá trị là
A. - 1 13
B. - 5 13
C. 5 13
D. 1 13
tính các tích phân
1.\(\int_{\dfrac{\pi}{4}}^{\dfrac{\pi}{2}}e^{\sin x}\cos xdx\)
2.\(\int_{\dfrac{\pi}{4}}^{\dfrac{\pi}{2}}e^{2\cos x+1}\sin xdx\)
3,\(\int_1^e\dfrac{e^{2lnx+1}}{x}dx\)
4.\(\int_0^1xe^{x^2+2}dx\)
Ở tất cả các dạng bài như thế này em chỉ cần ghi nhớ công thức:
\(d(u(x))=u'(x)dx\)
Câu 1)
Ta có \(I_1=\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} e^{\sin x}\cos xdx=\int _{\frac{\pi}{4}}^{\frac{\pi}{2}}e^{\sin x}d(\sin x)\)
Đặt \(\sin x=t\Rightarrow I_1=\int ^{1}_{\frac{\sqrt{2}}{2}}e^tdt=\left.\begin{matrix} 1\\ \frac{\sqrt{2}}{2}\end{matrix}\right|e^t=e-e^{\frac{\sqrt{2}}{2}}\)
Câu 2)
\(I_2=\int ^{\frac{\pi}{2}}_{\frac{\pi}{4}}e^{2\cos x+1}\sin xdx=\frac{-1}{2}\int ^\frac{\pi}{2}_{\frac{\pi}{4}}e^{2\cos x+1}d(2\cos x+1)\)
Đặt \(2\cos x+1=t\Rightarrow I_2=\frac{-1}{2}\int ^{1}_{1+\sqrt{2}}e^tdt\)
\(=\frac{-1}{2}.\left.\begin{matrix} 1\\ 1+\sqrt{2}\end{matrix}\right|e^t=\frac{-1}{2}(e-e^{1+\sqrt{2}})\)
Câu 3:
Có \(I_3=\int ^{e}_{1}\frac{e^{2\ln x+1}}{x}dx=\int ^{e}_{1}e^{2\ln x+1}d(\ln x)\)
\(=\frac{1}{2}\int ^{e}_{1}e^{2\ln x+1}d(2\ln x+1)\)
Đặt \(2\ln x+1=t\Rightarrow I_3=\frac{1}{2}\int ^{3}_{1}e^tdt=\frac{1}{2}.\left.\begin{matrix} 3\\ 1\end{matrix}\right|e^t=\frac{1}{2}(e^3-e)\)
Câu 4:
\(I_4=\int ^{1}_{0}xe^{x^2+2}dx=\frac{1}{2}\int ^{1}_{0}e^{x^2+2}d(x^2+2)\)
Đặt \(x^2+2=t\Rightarrow I_4=\frac{1}{2}\int ^{3}_{2}e^tdt=\frac{1}{2}.\left.\begin{matrix} 3\\ 2\end{matrix}\right|e^t=\frac{1}{2}(e^3-e^2)\)
tính nguyên hàm (sd pp nguyên hàm từng phần)
1. \(\int\dfrac{x}{\sin^2x}dx\)
2. \(\int\dfrac{x+1}{e^x}dx\)
3. \(\int x.\sin x.\cos xdx\)
4. \(\int e^x\sin xdx\)
1. Đặt \(\left\{{}\begin{matrix}u=x\\dv=\dfrac{dx}{sin^2x}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=dx\\v=-cotx\end{matrix}\right.\)
Do đó I= \(-x.cotx+\int cotxdx\)= \(-xcotx+ln\left|sinx\right|\)
2. Đặt \(\left\{{}\begin{matrix}u=x+1\\dv=\dfrac{dx}{e^x}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=dx\\v=-e^{-x}\end{matrix}\right.\)
Do đó I= \(-\left(x+1\right)e^{-x}+\int e^{-x}dx\)=\(-\left(x+1\right)e^{-x}-e^{-x}\)
=\(-\left(x+2\right)e^{-x}\)
3. Đặt \(\left\{{}\begin{matrix}u=x\\dv=sinx.cosx.dx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=dx\\dv=\dfrac{1}{4}sin2x.d\left(2x\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=\dfrac{-cos2x}{8}\end{matrix}\right.\), do đó I= \(\dfrac{-x.cos2x}{8}+\int\dfrac{cos2x}{8}dx\)
=\(\dfrac{-x.cos2x}{8}+\int\dfrac{cos2x}{16}d\left(2x\right)\)= \(\dfrac{-x.cos2x}{8}+\dfrac{sin2x}{32}\)
Cho hàm số f(x) liên tục trong đoạn [1;e], biết ∫ 1 e f ( x ) x d x = 1 ; f ( e ) = 2 Tích phân ∫ 1 e f ' ( x ) ln x d x
A. 1
B. 0
C. 2
D. 3
Cho hàm số f(x) liên tục trong đoạn [1;e], biết ∫ 1 e f ( x ) x d x = 1 , f(e) = 2. Tích phân ∫ 1 e f ' ( x ) ln x d x = ?
A. 1
B. 0
C. 2
D. 3
Đáp án A
Phương pháp: Công thức từng phần: ![]()
Cách giải:
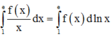
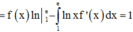
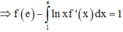
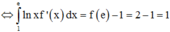
Tính các nguyên hàm sau đây :
a) \(\int\left(x+\ln x\right)x^2dx\)
b) \(\int\left(x+\sin^2x\right)\sin xdx\)
c) \(\int\left(x+e^x\right)e^{2x}dx\)
d) \(\int\left(x+\sin x\right)\dfrac{dx}{\cos^2x}\)
e) \(\int\dfrac{e^x\cos x+\left(e^x+1\right)\sin x}{e^x\sin x}dx\)
a) \(\int\left(x+\ln x\right)x^2\text{d}x=\int x^3\text{d}x+\int x^2\ln x\text{dx}\)
\(=\dfrac{x^4}{4}+\int x^2\ln x\text{dx}+C\) (*)
Để tính: \(\int x^2\ln x\text{dx}\) ta sử dụng công thức tính tích phân từng phần như sau:
Đặt \(\left\{{}\begin{matrix}u=\ln x\\v'=x^2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u'=\dfrac{1}{x}\\v=\dfrac{1}{3}x^3\end{matrix}\right.\)
Suy ra:
\(\int x^2\ln x\text{dx}=\dfrac{1}{3}x^3\ln x-\dfrac{1}{3}\int x^2\text{dx}\)
\(=\dfrac{1}{3}x^3\ln x-\dfrac{1}{3}.\dfrac{1}{3}x^3\)
Thay vào (*) ta tính được nguyên hàm của hàm số đã cho bằng:
(*) \(=\dfrac{1}{3}x^3-\dfrac{1}{3}x^3\ln x+\dfrac{1}{9}x^3+C\)
\(=\dfrac{4}{9}x^3-\dfrac{1}{3}x^3\ln x+C\)
b) Đặt \(\left\{{}\begin{matrix}u=x+\sin^2x\\v'=\sin x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u'=1+2\sin x.\cos x\\v=-\cos x\end{matrix}\right.\)
Ta có:
\(\int\left(x+\sin^2x\right)\sin x\text{dx}=-\left(x+\sin^2x\right)\cos x+\int\left(1+2\sin x\cos^2x\right)\text{dx}\)
\(=-\left(x+\sin^2x\right)\cos x+\int\cos x\text{dx}+2\int\sin x.\cos^2x\text{dx}\)
\(=-\left(x+\sin^2x\right)\cos x+\sin x-2\int\cos^2x.d\left(\cos x\right)\)
\(=-\left(x+\sin^2x\right)\cos x+\sin x-2\dfrac{\cos^3x}{3}+C\)
c) Đặt \(\left\{{}\begin{matrix}u=x+e^x\\v'=e^{2x}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u'=1+e^x\\v=\dfrac{1}{2}e^{2x}\end{matrix}\right.\)
Ta có:
\(\int\left(x+e^x\right)e^{2x}\text{dx}=\dfrac{1}{2}\left(x+e^x\right)e^{2x}-\dfrac{1}{2}\int\left(1+e^x\right)e^{2x}\text{dx}\)
\(=\dfrac{1}{2}\left(x+e^x\right)e^{2x}-\dfrac{1}{2}\int e^{2x}\text{dx}-\dfrac{1}{2}\int e^{3x}\text{dx}\)
\(=\dfrac{1}{2}\left(x+e^x\right)e^{2x}-\dfrac{1}{2}.\dfrac{1}{2}e^{2x}-\dfrac{1}{2}.\dfrac{1}{3}e^{3x}\)
\(=\dfrac{1}{2}xe^{2x}-\dfrac{1}{4}e^{2x}+\dfrac{1}{3}e^{3x}\)
Tính :
a) \(\int\limits^2_{-1}\left(5x^2-x+e^{0,5x}\right)dx\)
b) \(\int\limits^2_{0,5}\left(2\sqrt{x}+\dfrac{3}{x^2}+\cos x\right)dx\)
c) \(\int\limits^2_1\dfrac{dx}{\sqrt{2x+3}}\) (đặt \(t=\sqrt{2x+3}\) )
d) \(\int\limits^2_1\sqrt[3]{3x^3+4}x^2dx\) (đặt \(t=\sqrt[3]{3x^3+4}\) )
e) \(\int\limits^2_{-2}\left(x-2\right)\left|x\right|dx\)
g) \(\int\limits^0_1x\cos xdx\)
h) \(\int\limits^{\dfrac{\pi}{2}}_{\dfrac{\pi}{6}}\dfrac{1+\sin2x+\cos2x}{\sin x+\cos x}dx\)
i) \(\int\limits^{\dfrac{\pi}{2}}_0e^x\sin xdx\)
k) \(\int\limits^e_1x^2\ln^2xdx\)
Tính nguyên hàm:
1. \(\sqrt{3\cos x+2}\sin xdx\)( cả cụm 3cosx+2 trong căn hết nha)
2 \((1+sin^3x)cosx dx\)
3. \(e^x / \sqrt[]e^x-5\) ( mẫu trong căn hết nha)
4. \((xsinx+2)dx\)
5. \(2xcosxdx\)
6. 32 lnx dx
*Đặt tên các biểu thức theo thứ tự lần lượt là A,B,C,D,E,F *
Câu 1)
Ta có: \(d(\cos x)=(\cos x)'d(x)=-\sin xdx\)
\(\Rightarrow -d(\cos x)=\sin xdx\)
\(\Rightarrow A=\int \sqrt{3\cos x+2}\sin xdx=-\int \sqrt{3\cos x+2}d(\cos x)\)
Đặt \(\sqrt{3\cos x+2}=t\Rightarrow \cos x=\frac{t^2-2}{3}\)
\(\Rightarrow A=-\int td\left(\frac{t^2-2}{3}\right)=-\int t.\frac{2}{3}tdt=-\frac{2}{3}\int t^2dt=-\frac{2}{3}.\frac{t^3}{3}+c\)
\(=-\frac{2}{9}t^3+c=\frac{-2}{9}\sqrt{(3\cos x+2)^3}+c\)
Câu 2:
\(B=\int (1+\sin^3x)\cos xdx=\int \cos xdx+\int \sin ^3xcos xdx\)
\(=\int \cos xdx+\int \sin ^3xd(\sin x)\)
\(=\sin x+\frac{\sin ^4x}{4}+c\)
Câu 3:
\(C=\int \frac{e^x}{\sqrt{e^x-5}}dx=\int \frac{d(e^x)}{\sqrt{e^x-5}}\)
Đặt \(\sqrt{e^x-5}=t\Rightarrow e^x=t^2+5\)
Khi đó: \(C=\int \frac{d(t^2+5)}{t}=\int \frac{2tdt}{t}=\int 2dt=2t+c=2\sqrt{e^x-5}+c\)
Câu 4:
\(D=\int (x\sin x+2)dx=\int x\sin xdx+\int 2dx\)
Đặt \(\left\{\begin{matrix} u= x\\ dv= \sin xdx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=dx\\ v=\int \sin xdx=-\cos x \end{matrix}\right.\)
\(\Rightarrow \int x\sin xdx= -x\cos x+\int \cos xdx=-x\cos x+\sin x+c\)
\(\int 2dx=2x+c\)
Do đó: \(D=-x\cos x+\sin x+2x+c\)
Câu 5:
\(E=\int 2x\cos xdx=2\int x\cos xdx\)
Đặt \(\left\{\begin{matrix} u=x\\ dv=\cos xdx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=dx\\ v=\int \cos xdx=\sin x\end{matrix}\right.\)
\(\Rightarrow \int x\cos xdx=x\sin x-\int \sin xdx=x\sin x+\cos x+c\)
\(\Rightarrow E=2x\sin x+2\cos x+c\)
Câu 6:
\(\int 3^2\ln xdx=9\int \ln xdx\)
Đặt \(\left\{\begin{matrix} u=\ln x\\ dv=dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{dx}{x}\\ v=x\end{matrix}\right.\)
\(\Rightarrow \int \ln xdx=x\ln x-\int dx=x\ln x-x+c\)
\(\Rightarrow F=9x\ln x-9x+c\)
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính :
a) \(\int x\ln\left(1+x\right)dx\)
b) \(\int\left(x^2+2x-1\right)e^xdx\)
c) \(\int x\sin\left(2x+1\right)dx\)
d) \(\int\left(1-x\right)\cos xdx\)
a) Áp dụng phương pháp tìm nguyên hàm từng phần:
Đặt u= ln(1+x)
dv= xdx
=> ,
Ta có: ∫xln(1+x)dx =
=
b) Cách 1: Tìm nguyên hàm từng phần hai lần:
Đặt u= (x2+2x -1) và dv=exdx
Suy ra du = (2x+2)dx, v = ex
. Khi đó:
∫(x2+2x - 1)exdx = (x2+2x - 1)exdx - ∫(2x+2)exdx
Đặt : u=2x+2; dv=exdx
=> du = 2dx ;v=ex
Khi đó:∫(2x+2)exdx = (2x+2)ex - 2∫exdx = ex(2x+2) – 2ex+C
Vậy
∫(x2+2x+1)exdx = ex(x2-1) + C
Cách 2: HD: Ta tìm ∫(x2-1)exdx. Đặt u = x2-1 và dv=exdx.
Đáp số : ex(x2-1) + C
c) Đáp số:
HD: Đặt u=x ; dv = sin(2x+1)dx
d) Đáp số : (1-x)sinx - cosx +C.
HD: Đặt u = 1 - x ;dv = cosxdx
Tính :
a) \(\int\left(2-x\right)\sin xdx\)
b) \(\int\dfrac{\left(x+1\right)^2}{\sqrt{x}}dx\)
c) \(\int\dfrac{3^{3x}+1}{e^x+1}dx\)
d) \(\int\dfrac{1}{\left(\sin x+\cos x\right)^2}dx\)
e) \(\int\dfrac{1}{\sqrt{1+x}+\sqrt{x}}dx\)
g) \(\int\dfrac{1}{\left(1+x\right)\left(2-x\right)}dx\)
tích phân từ 0 đến 1 ( X^2 + 1 ) x e^xdx